统计学习方法|条件随机场模型原理详解与实现

条件随机场(CRF)，属于判别模型，它在自然语言处理领域用途非常广泛。由于其涉及较多的概率图模型的知识，所以，这篇博客将首先介绍一下关于CRF模型的提出的原因，接着再介绍CRF模型需要解决的问题，并针对每个问题介绍其解决的算法，最后将使用python与sklearn库来对其进行实现。

条件随机场模型提出的原因

如果用一句话来总结CRF被提出的原因就是：CRF解决了MEMM模型的标注偏差问题，打破了齐次markov假设，使得模型更加合理。（如果不想看分析过程的话，可以直接跳过，看第二部分CRF模型的介绍。）具体分析过程，如下：

分类模型

首先，我们可以大致看一下分类模型。整个分类模型可以被分为：硬分类与软分类。硬分类的代表模型有：感知机(PLA)、支持向量机(SVM)、线性判别分析(LDA)；软分类模型又可分为两类：判别模型与生成模型。判别模型的代表：逻辑回归(LR)模型以及最大熵(MaxEnt)模型；生成模型的代表：朴素贝叶斯(Naive Bayes)模型、隐马尔可夫(HMM)模型。之后，我们根据MaxEnt模型与HMM模型，可以得出一个判别模型——最大熵马尔可夫模型(MEMM)，最后在MEMM模型的基础上，得出了条件随机场(CRF)模型。

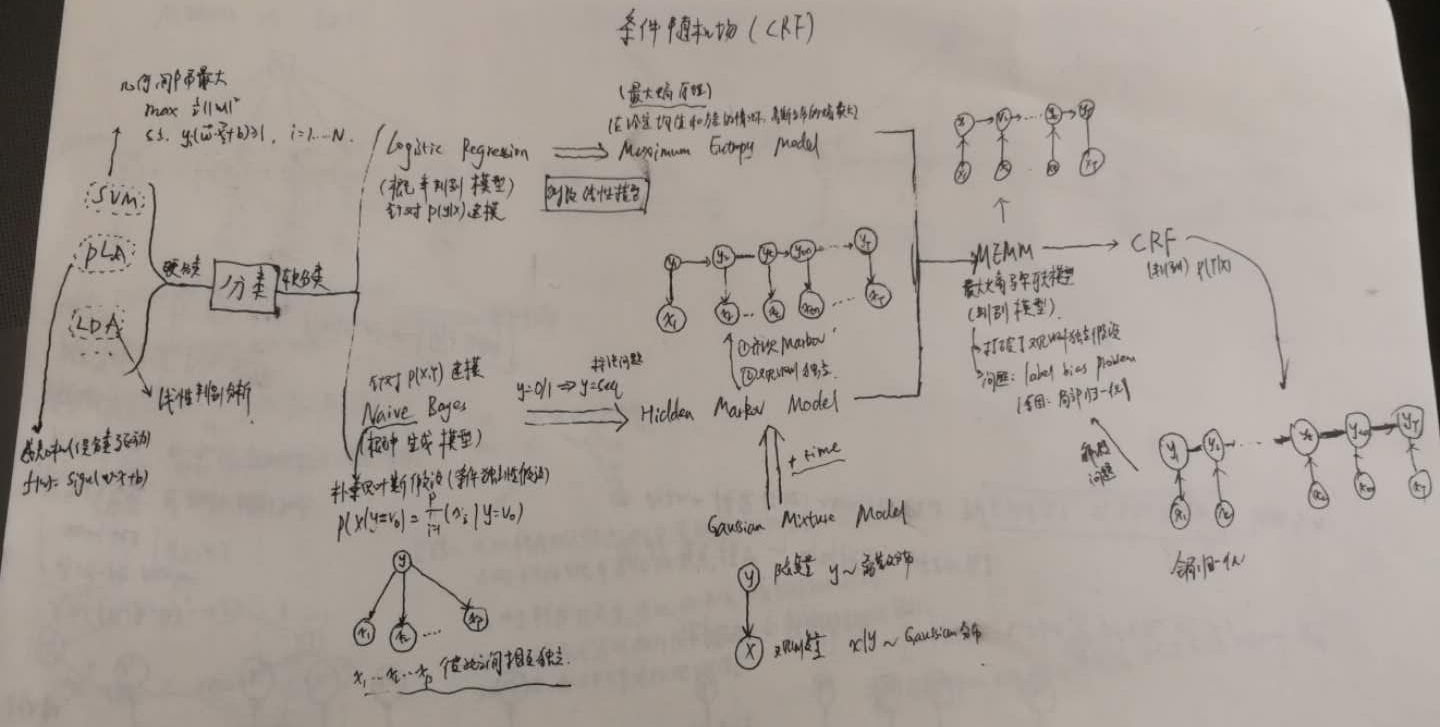
所以，CRF模型是从HMM到MEMM模型，一步步推出来的。那么，接下来，我们来具体看看是怎么得来的。

HMM vs MEMM

HMM模型，相信大家都很熟悉了，它可被用来解决词性标注等问题。HMM模型有两个很著名的假设：齐次一阶Markov假设与观测独立性假设。但是这两个假设都是合理的吗？其实不是的，如果对概率图模型的基本知识有些了解的话，我们会发现这两个假设其实都是为了简化运算。譬如说，我们来看观测独立性假设。它被描述为观测变量 $o_t$ 只与 $i_t$ 有关系，其实这是不合理的。以词性标注问题为例，单词与单词之间其实都是有关系的。那么，为了解决这个问题，MEMM模型便被提出来了，具体做法是：将原来的观测变量变为输入(从图的角度来说，就是剪箭头反向，具体为什么这样做就打破了观测独立性假设呢？其实和有向图的D-seperation有关，感兴趣的可以去了解了解这个)。MEMM的优点有：1.打破了观测独立性假设，使得模型更加合理；2.MEMM模型是判别模型，相比HMM模型来说，计算更为简单。但是MEMM模型也存在一个非常严重的缺陷：标注偏差问题(label bias problem)。这个问题会导致词性标注准确率大为降低。这也是MEMM模型没有流行的原因。

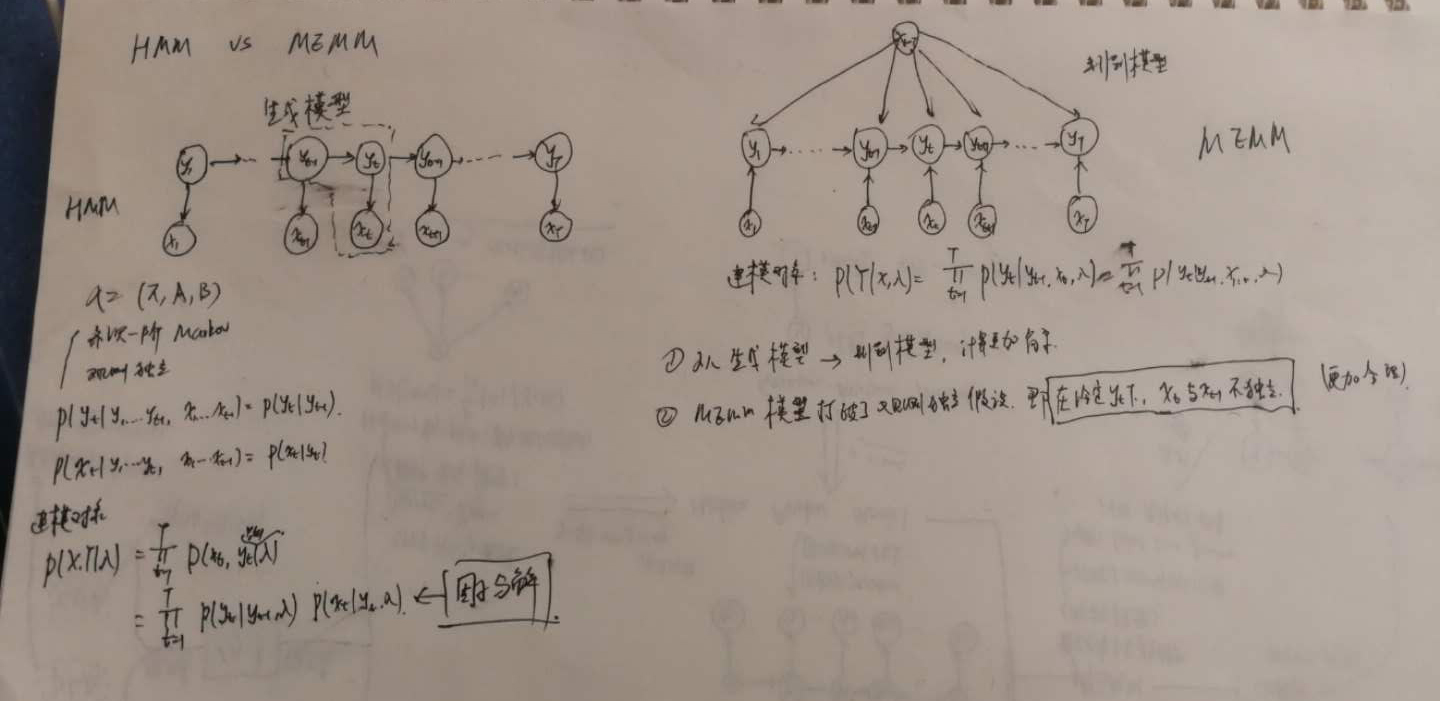
MEMM vs CRF

MEMM模型存在标注偏差问题，那么到底什么是标注偏差问题呢？(如果想深入了解的话，可以去看John Lafferty的那篇论文)。 如下：

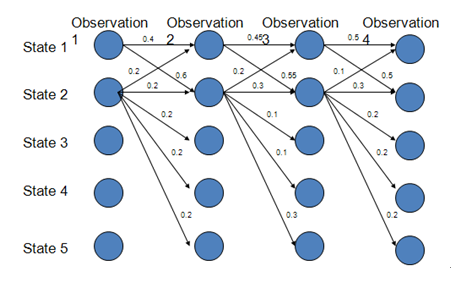
图中，每一列表示一个时刻，也就代表一个状态。当我们使用Viterbi算法去求具有最大概率的路径的时候，我们会得到1->2->2->2，概率是0.6*0.3*0.3=0.054，然而实际上最大概率的路径是:1->1->1->1，其概率是：0.4*0.45*0.5=0.09。那么，如果在词性标注问题中，就会导致标注发生错误。这就是标注偏差问题。那么导致这一问题的根本原因在于：局部归一化。也就是每一次从t时刻转移到t+1时刻的时候，都会对转移概率做归一化。从而，就会导致模型偏向于状态转移少的标签，从而使得后验概率最大，导致模型越不会去理睬观测变量的值，就会进行词性标注。

为了解决这一问题，就提出了CRF模型。CRF模型的具体做法是：将模型变成无向图，这样一来，就不需要在每一步都进行归一化，只需要进行全局归一化即可。这样，就解决了标注偏差问题。下面就讲具体介绍CRF模型。

条件随机场模型介绍

在介绍CRF之前，首先得先去了解有向图模型(贝叶斯网络)的因子分解与D-seperation，以及无向图(markov随机场)的D-separation(严格来讲，无向图没有D-seperation，但是它的结构和有向图的D-separation差不多，其实就是全局markov性)与因子分解。实际上，所谓的因子分解其实都是为了体现概率图模型的条件独立性。在无向图中，条件独立性表现在三个方面：全局markov性、局部markov性、成对markov性。那么因子分解为了表现其条件独立性，使用了基于团的方法，并有hammesley-Clifford定理得以保证。在这里，我就不详细讲了，如果讲的话，那就太多太多啦～感兴趣的同学可以去补补概率图的知识，就按照我上面讲的这些即可～

OK，直接进入主题。

CRF模型是给定随机变量$X$的条件下，随机变量$Y$的markov随机场。其概率图如下：

由于CRF模型是判别式模型，所以建模对象就是：$P(Y|X)$。也就是说，我们要求的是$P(Y|X)$。下面我们就来推导一下线性链CRF的参数形式。如下：

所以，我们现在得到了CRF的参数形式，当随机变量$X$取$x$，随机变量$Y$取$y$的时候，如下：

$$P(y|x)=\frac {1}{z}exp\sum_{t=1}^{T}[\sum_{k=1}^{K}\lambda_kf_k(y_{t-1},y_t,x_{1:T})+\sum_{l=1}^{L}\eta_lg_l(y_t,x_{1:T})]$$

其中，$\lambda、\eta$ 都是需要训练的参数，$f、g$ 是特征函数，当满足某一条件的时候，为1，否则为0。在这里，需要注意的是，我所使用的符号与李航老师的《统计学习方法》不太一样，但是表达都是一样的，《统计学习方法》中将最外面的那个$\sum$放进去了，所以特征函数的参数就会多一个。其实都是一样的，我觉得最重要的是自己能够理解，并且方便自己记忆和推导就可以了：

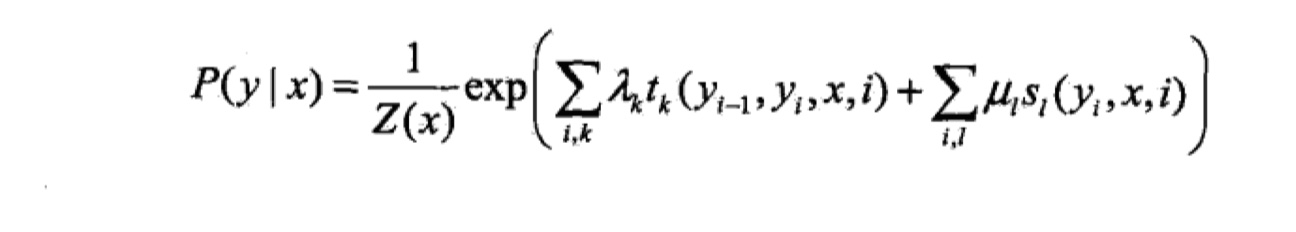
那么，我们使用将其化简为向量化的形式，如下：

所以，我们就得到了CRF的向量化形式：

$$P(y|x)=\frac {1}{z(x,\theta)}exp[\theta^T(H(y_{t-1},y_t,x)]$$

那么，得到这个之后，我们就来解决CRF模型中的问题。CRF总共需要解决三个问题：

• 求边缘概率。即：求$P(y_t|x)$。
• 学习问题。即：给定训练集$\{x^{(i)},y^{(i)}\}_1^N$，求：$\theta=\mathop{argmax}\limits_{\theta}\prod_{i=1}^{N}P(y^{(i)}|x^{(i)})$。N个样本，其中x都是T维的。
• Decoding问题。即：求：$y=\mathop{argmax}\limits_{y}P(y|x)$。

边缘概率问题的求解

在这里，其实计算过程与HMM中的概率计算其实是一样的，同样引进前向后向算法，来减小计算复杂度。具体推导过程如下（推导过程采用了变量消除法）：

我们可以看到，原来的计算复杂度为：$O(T|S|^T)$。当$T$很大的时候，复杂度是以指数形式增长的，这是不可解的。当我们已经引进前向向量与后向向量，那么就可解了。

模型参数的求解

关于CRF模型参数的求解方法，其实有很多。比如有：改进的迭代尺度法、拟牛顿法、牛顿法等等。在这里，我采用的是梯度上升法，因为是求最大，当然也可以将其转换为求最小问题，使用梯度下降法来解决。其实过程差不多的。具体推导过程如下(原谅我手机的渣渣像素，以后有时间再用markdown把公式打出来吧😩)：

Decoding问题的求解

每次写博客，都感觉好累🥱。CRF的decoding问题，仍然是使用Viterbi算法进行求解，在这里，我就不推导了，直接放《统计学习方法》的截图吧，如果你之前看过我关于HMM模型的讲解那一篇的话，那么CRF的Viterbi算法也绝对能看得懂～

至此，关于CRF的理论部分就讲完了～

CRF模型的实现

把模型实现一遍才算是真正的吃透了这个模型呀。在这里，我采取了两种方式来实现CRF模型：python实现以及调用scikit-learn库来实现。我的github里面可以下在到所有的代码，欢迎访问我的github，也欢迎大家star和fork。附上GitHub地址: 《统计学习方法》及常规机器学习模型实现。具体代码如下：

python实现

#coding:utf-8
#Author:codewithzichao
#E-mail:lizichao@pku.edu.cn

'''
由于CRF模型，一般都是来解决其Decoding问题，所以在此，我只实现Viterbi算法～
'''

import numpy as np


class CRF(object):
    '''实现条件随机场预测问题的维特比算法
    '''

    def __init__(self, V, VW, E, EW):
        '''
        :param V:是定义在节点上的特征函数，称为状态特征
        :param VW:是V对应的权值
        :param E:是定义在边上的特征函数，称为转移特征
        :param EW:是E对应的权值
        '''
        self.V = V  # 点分布表
        self.VW = VW  # 点权值表
        self.E = E  # 边分布表
        self.EW = EW  # 边权值表
        self.D = []  # Delta表，最大非规范化概率的局部状态路径概率
        self.P = []  # Psi表，当前状态和最优前导状态的索引表s
        self.BP = []  # BestPath，最优路径
        return

    def Viterbi(self):
        '''
        条件随机场预测问题的维特比算法，此算法一定要结合CRF参数化形式对应的状态路径图来理解，更容易理解.
        '''
        self.D = np.full(shape=(np.shape(self.V)), fill_value=.0)
        self.P = np.full(shape=(np.shape(self.V)), fill_value=.0)
        for i in range(np.shape(self.V)[0]):
            # 初始化
            if 0 == i:
                self.D[i] = np.multiply(self.V[i], self.VW[i])
                self.P[i] = np.array([0, 0])
                print('self.V[%d]=' % i, self.V[i], 'self.VW[%d]=' % i, self.VW[i], 'self.D[%d]=' % i, self.D[i])
                print('self.P:', self.P)
                pass
            # 递推求解布局最优状态路径
            else:
                for y in range(np.shape(self.V)[1]):  # delta[i][y=1,2...]
                    for l in range(np.shape(self.V)[1]):  # V[i-1][l=1,2...]
                        delta = 0.0
                        delta += self.D[i - 1, l]  # 前导状态的最优状态路径的概率
                        delta += self.E[i - 1][l, y] * self.EW[i - 1][l, y]  # 前导状态到当前状体的转移概率
                        delta += self.V[i, y] * self.VW[i, y]  # 当前状态的概率
                        print('(x%d,y=%d)-->(x%d,y=%d):%.2f + %.2f + %.2f=' % (i - 1, l, i, y, \
                                                                               self.D[i - 1, l], \
                                                                               self.E[i - 1][l, y] * self.EW[i - 1][
                                                                                   l, y], \
                                                                               self.V[i, y] * self.VW[i, y]), delta)
                        if 0 == l or delta > self.D[i, y]:
                            self.D[i, y] = delta
                            self.P[i, y] = l
                    print('self.D[x%d,y=%d]=%.2f\n' % (i, y, self.D[i, y]))
        print('self.Delta:\n', self.D)
        print('self.Psi:\n', self.P)

        # 返回，得到所有的最优前导状态
        N = np.shape(self.V)[0]
        self.BP = np.full(shape=(N,), fill_value=0.0)
        t_range = -1 * np.array(sorted(-1 * np.arange(N)))
        for t in t_range:
            if N - 1 == t:  # 得到最优状态
                self.BP[t] = np.argmax(self.D[-1])
            else:  # 得到最优前导状态
                self.BP[t] = self.P[t + 1, int(self.BP[t + 1])]

        # 最优状态路径表现在存储的是状态的下标，我们执行存储值+1转换成示例中的状态值
        # 也可以不用转换，只要你能理解，self.BP中存储的0是状态1就可以~~~~
        self.BP += 1

        print('最优状态路径为：', self.BP)
        return self.BP



if __name__ == '__main__':
    S = np.array([[1, 1],  # X1:S(Y1=1), S(Y1=2)
                  [1, 1],  # X2:S(Y2=1), S(Y2=2)
                  [1, 1]])  # X3:S(Y3=1), S(Y3=1)
    SW = np.array([[1.0, 0.5],  # X1:SW(Y1=1), SW(Y1=2)
                   [0.8, 0.5],  # X2:SW(Y2=1), SW(Y2=2)
                   [0.8, 0.5]])  # X3:SW(Y3=1), SW(Y3=1)
    E = np.array([[[1, 1],  # Edge:Y1=1--->(Y2=1, Y2=2)
                   [1, 0]],  # Edge:Y1=2--->(Y2=1, Y2=2)
                  [[0, 1],  # Edge:Y2=1--->(Y3=1, Y3=2)
                   [1, 1]]])  # Edge:Y2=2--->(Y3=1, Y3=2)
    EW = np.array([[[0.6, 1],  # EdgeW:Y1=1--->(Y2=1, Y2=2)
                    [1, 0.0]],  # EdgeW:Y1=2--->(Y2=1, Y2=2)
                   [[0.0, 1],  # EdgeW:Y2=1--->(Y3=1, Y3=2)
                    [1, 0.2]]])  # EdgeW:Y2=2--->(Y3=1, Y3=2)

    crf = CRF(S, SW, E, EW)
    ret = crf.Viterbi()
    print('最优状态路径为:', ret)

sklearn实现

#coding:utf-8
#Author:codewithzichao
#E-mail:lizichao@pku.edu.cn

'''
训练数据集：1998人民日报标注语料库
目标：对其进行命名实体识别
结果：
数据：新华社北京十二月三十一日电(中央人民广播电台记者刘振英、新华社记者张宿堂)今天是一九九七年的最后一天。
结果：新华社 北京 十二月三十一日  中央人民广播电台  刘振英  新华社  张宿堂  今天  一九九七年
----------------------------------------------------------
数据：中国，我爱你。
结果：中国
来源：https://www.jianshu.com/p/7fa260e91382
'''


import re
import sklearn_crfsuite
from sklearn_crfsuite import metrics
import joblib


class CorpusProcess(object):

    def __init__(self):
        """初始化"""
        self.train_corpus_path ="1980_01.txt"
        self.process_corpus_path ="result-rmrb.txt"
        self._maps = {u't': u'T', u'nr': u'PER', u'ns': u'ORG', u'nt': u'LOC'}

    def read_corpus_from_file(self, file_path):
        """读取语料"""
        f = open(file_path, 'r', encoding='utf-8')
        lines = f.readlines()
        f.close()
        return lines

    def write_corpus_to_file(self, data, file_path):
        """写语料"""
        f = open(file_path, 'wb')
        f.write(data)
        f.close()

    def q_to_b(self, q_str):
        """全角转半角"""
        b_str = ""
        for uchar in q_str:
            inside_code = ord(uchar)
            if inside_code == 12288:  # 全角空格直接转换
                inside_code = 32
            elif 65374 >= inside_code >= 65281:  # 全角字符（除空格）根据关系转化
                inside_code -= 65248
            b_str += chr(inside_code)
        return b_str

    def b_to_q(self, b_str):
        """半角转全角"""
        q_str = ""
        for uchar in b_str:
            inside_code = ord(uchar)
            if inside_code == 32:  # 半角空格直接转化
                inside_code = 12288
            elif 126 >= inside_code >= 32:  # 半角字符（除空格）根据关系转化
                inside_code += 65248
            q_str += chr(inside_code)
        return q_str

    def pre_process(self):
        """语料预处理 """
        lines = self.read_corpus_from_file(self.train_corpus_path)
        new_lines = []
        for line in lines:
            words = self.q_to_b(line.strip()).split(u'  ')
            pro_words = self.process_t(words)
            pro_words = self.process_nr(pro_words)
            pro_words = self.process_k(pro_words)
            new_lines.append('  '.join(pro_words[1:]))
        self.write_corpus_to_file(data='\n'.join(new_lines).encode('utf-8'), file_path=self.process_corpus_path)

    def process_k(self, words):
        """处理大粒度分词,合并语料库中括号中的大粒度分词,类似：[国家/n  环保局/n]nt """
        pro_words = []
        index = 0
        temp = u''
        while True:
            word = words[index] if index < len(words) else u''
            if u'[' in word:
                temp += re.sub(pattern=u'/[a-zA-Z]*', repl=u'', string=word.replace(u'[', u''))
            elif u']' in word:
                w = word.split(u']')
                temp += re.sub(pattern=u'/[a-zA-Z]*', repl=u'', string=w[0])
                pro_words.append(temp + u'/' + w[1])
                temp = u''
            elif temp:
                temp += re.sub(pattern=u'/[a-zA-Z]*', repl=u'', string=word)
            elif word:
                pro_words.append(word)
            else:
                break
            index += 1
        return pro_words

    def process_nr(self, words):
        """ 处理姓名，合并语料库分开标注的姓和名，类似：温/nr  家宝/nr"""
        pro_words = []
        index = 0
        while True:
            word = words[index] if index < len(words) else u''
            if u'/nr' in word:
                next_index = index + 1
                if next_index < len(words) and u'/nr' in words[next_index]:
                    pro_words.append(word.replace(u'/nr', u'') + words[next_index])
                    index = next_index
                else:
                    pro_words.append(word)
            elif word:
                pro_words.append(word)
            else:
                break
            index += 1
        return pro_words

    def process_t(self, words):
        """处理时间,合并语料库分开标注的时间词，类似： （/w  一九九七年/t  十二月/t  三十一日/t  ）/w   """
        pro_words = []
        index = 0
        temp = u''
        while True:
            word = words[index] if index < len(words) else u''
            if u'/t' in word:
                temp = temp.replace(u'/t', u'') + word
            elif temp:
                pro_words.append(temp)
                pro_words.append(word)
                temp = u''
            elif word:
                pro_words.append(word)
            else:
                break
            index += 1
        return pro_words

    def pos_to_tag(self, p):
        """由词性提取标签"""
        t = self._maps.get(p, None)
        return t if t else u'O'

    def tag_perform(self, tag, index):
        """标签使用BIO模式"""
        if index == 0 and tag != u'O':
            return u'B_{}'.format(tag)
        elif tag != u'O':
            return u'I_{}'.format(tag)
        else:
            return tag

    def pos_perform(self, pos):
        """去除词性携带的标签先验知识"""
        if pos in self._maps.keys() and pos != u't':
            return u'n'
        else:
            return pos

    def initialize(self):
        """初始化 """
        lines = self.read_corpus_from_file(self.process_corpus_path)
        words_list = [line.strip().split('  ') for line in lines if line.strip()]
        del lines
        self.init_sequence(words_list)

    def init_sequence(self, words_list):
        """初始化字序列、词性序列、标记序列 """
        words_seq = [[word.split(u'/')[0] for word in words] for words in words_list]
        pos_seq = [[word.split(u'/')[1] for word in words] for words in words_list]
        tag_seq = [[self.pos_to_tag(p) for p in pos] for pos in pos_seq]
        self.pos_seq = [[[pos_seq[index][i] for _ in range(len(words_seq[index][i]))]
                         for i in range(len(pos_seq[index]))] for index in range(len(pos_seq))]
        self.tag_seq = [[[self.tag_perform(tag_seq[index][i], w) for w in range(len(words_seq[index][i]))]
                         for i in range(len(tag_seq[index]))] for index in range(len(tag_seq))]
        self.pos_seq = [[u'un'] + [self.pos_perform(p) for pos in pos_seq for p in pos] + [u'un'] for pos_seq in
                        self.pos_seq]
        self.tag_seq = [[t for tag in tag_seq for t in tag] for tag_seq in self.tag_seq]
        self.word_seq = [[u'<BOS>'] + [w for word in word_seq for w in word] + [u'<EOS>'] for word_seq in words_seq]

    def extract_feature(self, word_grams):
        """特征选取"""
        features, feature_list = [], []
        for index in range(len(word_grams)):
            for i in range(len(word_grams[index])):
                word_gram = word_grams[index][i]
                feature = {u'w-1': word_gram[0], u'w': word_gram[1], u'w+1': word_gram[2],
                           u'w-1:w': word_gram[0] + word_gram[1], u'w:w+1': word_gram[1] + word_gram[2],
                           # u'p-1': self.pos_seq[index][i], u'p': self.pos_seq[index][i+1],
                           # u'p+1': self.pos_seq[index][i+2],
                           # u'p-1:p': self.pos_seq[index][i]+self.pos_seq[index][i+1],
                           # u'p:p+1': self.pos_seq[index][i+1]+self.pos_seq[index][i+2],
                           u'bias': 1.0}
                feature_list.append(feature)
            features.append(feature_list)
            feature_list = []
        return features

    def segment_by_window(self, words_list=None, window=3):
        """窗口切分"""
        words = []
        begin, end = 0, window
        for _ in range(1, len(words_list)):
            if end > len(words_list): break
            words.append(words_list[begin:end])
            begin = begin + 1
            end = end + 1
        return words

    def generator(self):
        """训练数据"""
        word_grams = [self.segment_by_window(word_list) for word_list in self.word_seq]
        features = self.extract_feature(word_grams)
        return features, self.tag_seq



class CRF_NER(object):

    def __init__(self):
        """初始化参数"""
        self.algorithm = "lbfgs"
        self.c1 = "0.1"
        self.c2 = "0.1"
        self.max_iterations = 100
        self.model_path ="model.pkl"
        self.corpus = CorpusProcess()  # Corpus 实例
        self.corpus.pre_process()  # 语料预处理
        self.corpus.initialize()  # 初始化语料
        self.model = None

    def initialize_model(self):
        """初始化"""
        algorithm = self.algorithm
        c1 = float(self.c1)
        c2 = float(self.c2)
        max_iterations = int(self.max_iterations)
        self.model = sklearn_crfsuite.CRF(algorithm=algorithm, c1=c1, c2=c2,
                                          max_iterations=max_iterations, all_possible_transitions=True)

    def train(self):
        """训练"""
        self.initialize_model()
        x, y = self.corpus.generator()
        x_train, y_train = x[500:], y[500:]
        x_test, y_test = x[:500], y[:500]
        self.model.fit(x_train, y_train)
        labels = list(self.model.classes_)
        labels.remove('O')
        y_predict = self.model.predict(x_test)
        metrics.flat_f1_score(y_test, y_predict, average='weighted', labels=labels)
        sorted_labels = sorted(labels, key=lambda name: (name[1:], name[0]))
        print(metrics.flat_classification_report(y_test, y_predict, labels=sorted_labels, digits=3))
        self.save_model()

    def predict(self, sentence):
        """预测"""
        self.load_model()
        u_sent = self.corpus.q_to_b(sentence)
        word_lists = [[u'<BOS>'] + [c for c in u_sent] + [u'<EOS>']]
        word_grams = [self.corpus.segment_by_window(word_list) for word_list in word_lists]
        features = self.corpus.extract_feature(word_grams)
        y_predict = self.model.predict(features)
        entity = u''
        for index in range(len(y_predict[0])):
            if y_predict[0][index] != u'O':
                if index > 0 and y_predict[0][index][-1] != y_predict[0][index - 1][-1]:
                    entity += u' '
                entity += u_sent[index]
            elif entity[-1] != u' ':
                entity += u' '
        return entity

    def load_model(self):
        """加载模型 """
        self.model = joblib.load(self.model_path)

    def save_model(self):
        """保存模型"""
        joblib.dump(self.model, self.model_path)


if __name__=="__main__":

    ner = CRF_NER()
    #训练模型，当训练完毕后，就可以直接加载模型参数，不用再次训练了
    #mode=ner.train()

    result1=ner.predict(u'新华社北京十二月三十一日电(中央人民广播电台记者刘振英、新华社记者张宿堂)今天是一九九七年的最后一天。')
    print(result1)
    result2=ner.predict(u'中国，我爱你。')
    print(result2)