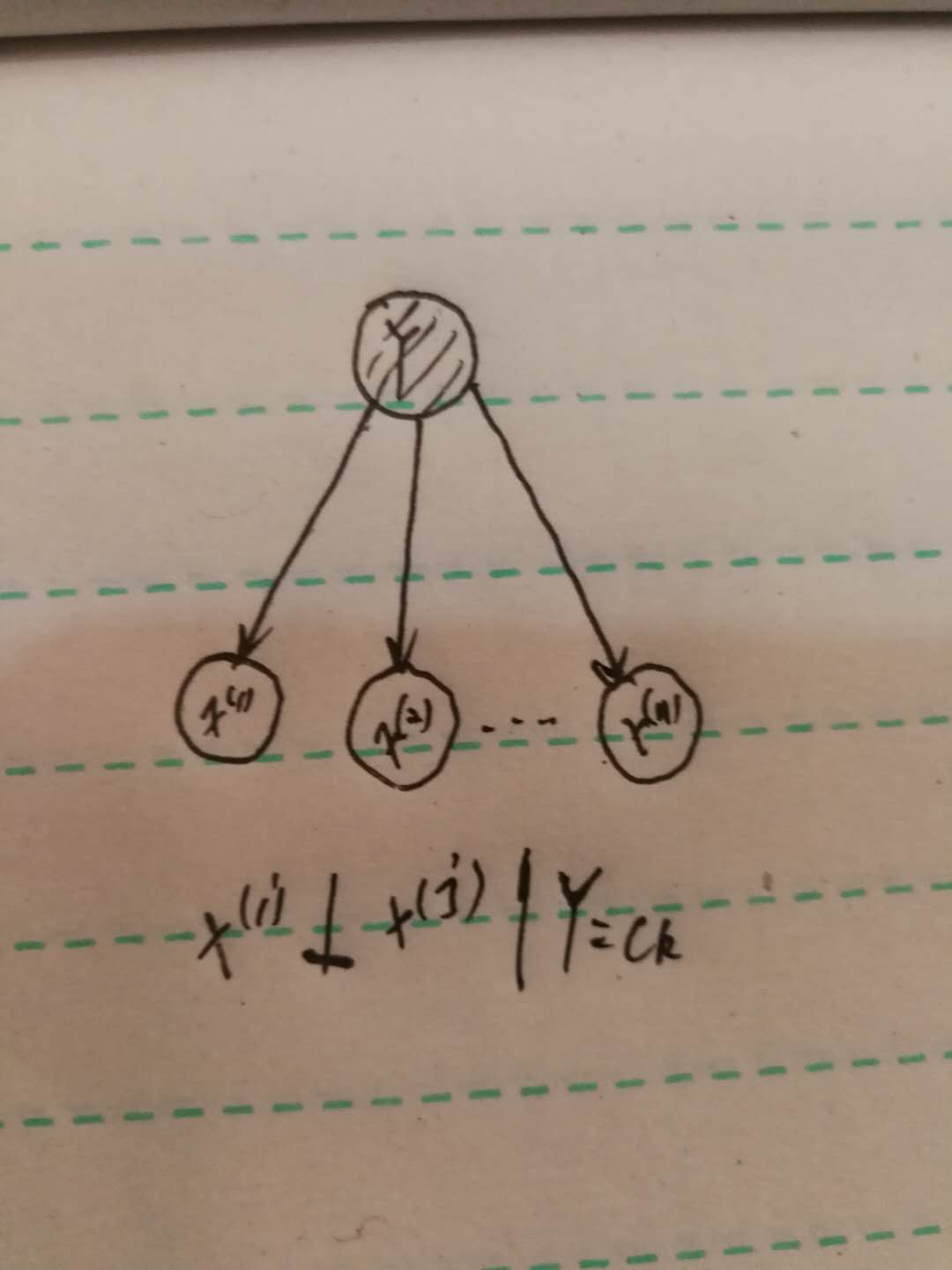Confident，Modest，Patient

0%

统计学习方法|朴素贝叶斯模型详解与实现

Posted on Edited on In

朴素贝叶斯模型(naive bayes)属于分类模型，也是最为简单的概率图模型，对于之后理解HMM、CRF等模型，大有裨益。本篇博客将对朴素贝叶斯模型的原理进行详细的讲解，并采用纯python实现以及调用scikit-learn库实现，这两种方式对朴素贝叶斯模型进行实现。

朴素贝叶斯模型概述

在朴素贝叶斯中，我们最终的目标是：给定实例的特征向量$X=x$，求得实例的类别标签$Y$，即求令$ P(Y=c_k|X) $值最大的类别标签$c_k$。那么怎么做呢？我们会通过求先验概率$P(Y)$与条件概率$P(X|Y)$，得到联合概率分布(也就是说朴素贝叶斯模型属于生成模型)，最后根据贝叶斯定理求得$P(Y|X)$，从中选择$P(Y=c_k|X)$的值最大的类别标签$c_k$，整个过程就结束了。如果我们仔细观察这个过程的话，我们会发现有几个问题需要解决：1.先验概率$P(Y)$与条件概率$P(X|Y)$怎么求出的？ 2. 如果实例的特征向量特别多的话，会造成计算量特别大，怎么解决的？下面我们将一一介绍。

朴素贝叶斯的两大前提条件

贝叶斯定理。贝叶斯定理，相信大家应该特别熟悉。假设$X$是特征向量，$Y$是类别标签，有$K$种取值，我们要通过$X$来预测$Y$。那么如下：

其中，$P(Y)$叫做先验概率，$P(X|Y)$叫做条件概率，$P(Y|X)$叫做后验概率。

条件独立性假设。假设每个实例特征向量有$n$维的话，第$j$个特征有$S_j$个取值。我们假设特征之间都是相互独立的，那么有

条件独立性假设是非常强的假设，主要目的就是为了简化运算，实际上，特征之间应该是有关系的才更合理一些。而如果没有这个假设的话，那么上式的参数实际有:$K\prod_{j=1}^{n}S_j$，当特征维度特别大的时候，这个参数量是非常大的。当采用了这个假设之后，参数量就变为：$K\sum_{j=1}^{n}S_j$，这样就小很多。如果采用概率图来表示的话，如下图：

我们可以简单理解为：给定$Y=c_k$，两个特征之间，由于被$Y$给阻断了，所以彼此独立。

那么，根据上面两大前提条件，我们可以得到朴素贝叶斯模型。实际上我们就是要最大化后验概率，从而得到类别标签。如下：

由于$P(X=x)$对于所有的类别标签来说的话，都是一样的，所以可以去掉，最终得到的公式如下:

这就是朴素贝叶斯公式，是不是非常简单～

先验概率与条件概率的计算

当得到了朴素贝叶斯的公式后，那么其中的$P(Y=c_k)$与$P(X=x|Y=c_k)$怎么求呢？在这里，我们需要分情况讨论：得看特征本身是离散的还是连续的。当特征是离散的时候，我们使用极大似然估计，叫做多项式模型；当特征是连续的时候，我们让其满足高斯分布，叫做高斯模型。下面就一一介绍。

多项式模型

当特征是离散的时候，我们使用极大似然估计去得到先验概率与条件概率。（公式太难敲了，我就直接贴图了😭图片来源：《统计学习方法》）

但是，在计算先验概率与条件概率的时候，我们会做一些平滑处理，以防出现为0的情况，从而影响到后验概率的计算。这种操作叫做laplace平滑。（图片来源：《统计学习方法》）

高斯模型

当特征为连续值的时候，我们就不能采取多项式模型来估计先验概率与条件概率了，因为会导致很多$P(X=x_i|Y=c_k)$等于0。所以需要采用高斯模型。高斯模型的思想是：让特征的每一维都满足高斯分布(正态分布)，从而来处理连续特征。注意，先验概率的计算与多项式模型相同。公式如下：

其中，$\sigma^{2}_{c_k,j}$表示类别是$c_k$的实例中，第$j$维特征的方差，$\mu_{c_k,j}$表示类别是$c_k$的实例中，第$j$维特征的均值。

当求出先验概率与条件概率之后，再带入到朴素贝叶斯公式中，就可以得到实例的类别标签了。到此，朴素贝叶斯的理论部分就讲完啦，相较于HMM、CRF等模型，真的可以说是非常简单了🎉～

朴素贝叶斯模型的实现

把模型实现一遍才算是真正的吃透了这个模型呀。在这里，我采取了两种方式来实现朴素贝叶斯模型：纯python实现以及调用scikit-learn库来实现。我的github里面可以下载到所有的代码，欢迎访问我的github，也欢迎大家star和fork。附上GitHub地址: 《统计学习方法》及常规机器学习模型实现。具体代码如下：

python实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
# coding=utf-8
# Author:codewithzichao
# E-mail:lizichao@pku.edu.cn
# Date:2019-12-30

'''
数据集：Mnist
准确率：0.8433
时间：130.05937218666077
'''

import numpy  as np
import time


def loadData(fileName):
    data_list = []
    label_list = []
    with open(fileName, "r") as f:
        for line in f.readlines():
            curline = line.strip().split(",")
            label_list.append(int(curline[0]))
            data_list.append([int(int(feature) > 128) for feature in curline[1:]])  # 二值化，保证每一个特征只能取到0和1两个值

    data_matrix = np.array(data_list)
    label_matrix = np.array(label_list)

    return data_matrix, label_matrix


class Naive_Bayes(object):
    def __init__(self, train_data, train_label):
        '''
        构造函数
        :param train_data:训练集的特征向量
        :param train_label: 训练集的类别标签
        '''
        self.train_data = train_data
        self.train_label = train_label
        self.input_num, self.feature_num = self.train_data.shape  # input_num、feature_num表示训练集数目、特征数目
        self.classes_num = self.count_classes()
        self.p_y, self.p_x_y = self.get_probabilities()

    def count_classes(self):
        '''
        计算类别数目
        :return:类别数
        '''
        s = set()
        for i in self.train_label:
            if i not in s:
                s.add(i)
        return len(s)

    def get_probabilities(self):
        '''
        计算先验概率与条件概率
        :return: 返回先验概率与条件概率
        '''
        print("start training")
        p_y = np.zeros(self.classes_num)
        p_x_y = np.zeros((self.classes_num, self.input_num, 2))

        # 计算先验概率p_y
        for i in range(self.classes_num):
            p_y[i] = (np.sum((self.train_label == i)) + 1) / (self.input_num + self.classes_num)
        p_y = np.log(p_y)

        # 计算条件概率
        for i in range(self.input_num):
            label = self.train_label[i]
            x = self.train_data[i]
            for j in range(self.feature_num):
                p_x_y[label][j][x[j]] += 1

        for i in range(self.classes_num):
            for j in range(self.feature_num):
                p_x_y_0 = p_x_y[i][j][0]
                p_x_y_1 = p_x_y[i][j][1]

                p_x_y[i][j][0] = np.log((p_x_y_0 + 1) / (p_x_y_0 + p_x_y_1 + 2))
                p_x_y[i][j][1] = np.log((p_x_y_1 + 1) / (p_x_y_0 + p_x_y_1 + 2))
        print("finished training.")
        return p_y, p_x_y

    def naive_bayes_predict(self, x):
        '''
        预测单个实例x的类别标签
        :param x: 特征向量
        :return: x的类别标签
        '''

        p = np.zeros(self.classes_num)
        p_y, p_x_y = self.p_y, self.p_x_y

        for i in range(self.classes_num):
            for j in range(self.feature_num):
                p[i] += p_x_y[i][j][x[j]]
            p[i] += p_y[i]

        return np.argmax(p)

    def test_model(self, test_train, test_label):
        '''
        在整个测试集上测试模型
        :param test_train: 测试集的特征向量
        :param test_label: 测试集的类别标签
        :return: 准确率
        '''
        print("start testing")
        error = 0
        for i in range(len(test_label)):
            if (self.naive_bayes_predict(test_train[i]) != test_label[i]):
                error += 1
            else:
                continue

        accuarcy = (len(test_label) - error) / (len(test_label))
        print("finished testing.")
        return accuarcy


if __name__ == "__main__":
    start = time.time()

    print("start loading data.")
    train_data, train_label = loadData("../MnistData/mnist_train.csv")
    test_data, test_label = loadData("../MnistData/mnist_test.csv")
    print("finished load data.")

    a = Naive_Bayes(train_data, train_label)
    accuracy = a.test_model(test_data, test_label)
    print(f"the accuracy is {accuracy}.")

    end = time.time()
    print(f"the total time is {end - start}.")

sckit-learn实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
# coding=utf-8
# Author:codewithzichao
# E-mail:lizichao@pku.edu.cn
# Date:2019-12-30

import numpy as np
from sklearn.naive_bayes import MultinomialNB
from sklearn.metrics import classification_report

def loadData(fileName):
    data_list = []
    label_list = []
    with open(fileName, "r") as f:
        for line in f.readlines():
            curline = line.strip().split(",")
            label_list.append(int(curline[0]))
            data_list.append([int(int(feature) > 128) for feature in curline[1:]])  # 二值化，保证每一个特征只能取到0和1两个值

    data_matrix = np.array(data_list)
    label_matrix = np.array(label_list)

    return data_matrix, label_matrix

if __name__=="__main__":

    print("start loading data.")
    train_data, train_label = loadData("../MnistData/mnist_train.csv")
    test_data, test_label = loadData("../MnistData/mnist_test.csv")
    print("finished load data.")

    clf=MultinomialNB()
    clf.fit(train_data,train_label)

    accuracy=clf.score(test_data,test_label)

    print(f"the accuracy is {accuracy}.")

    test_predict=clf.predict(test_data)
    print(classification_report(test_label, test_predict))

Would you like to buy me a cup of coffee☕️～