感知机模型(perceptron)可以说是机器学习中最为简单的模型之一,也是之后的神经网络的原型与基础。本篇博客将对感知机模型的原理进行详细的讲解,并采用纯python实现以及调用scikit-learn库实现,这两种方式对感知机模型进行实现。
感知机模型概述 感知机模型是二分类的模型,属于监督学习的范畴。当输入实例的特征向量到感知机模型 中后,模型能够输出实例的类别(1或者-1)。所以,感知机的核心在于找到能够完全正确分离正类与负类的分离超平面。那么,为了能够求得此分离超平面,我们需要定义学习策略 。在感知机中,定义了误分类驱动的损失函数,并采用随机梯度下降算法 ,对损失函数进行求解。下面,将从模型、策略、算法 三方面,依此对感知机进行详细地讲解。
感知机模型 感知机模型如下:
其中,$x$是模型输入,$y$是模型输出,并且$x\in R^n,y\in \{1,-1\}$;$w,b$是模型参数,并且$w\in R^n,b\in R$。那么该模型是什么意思呢?可以做如下解释:
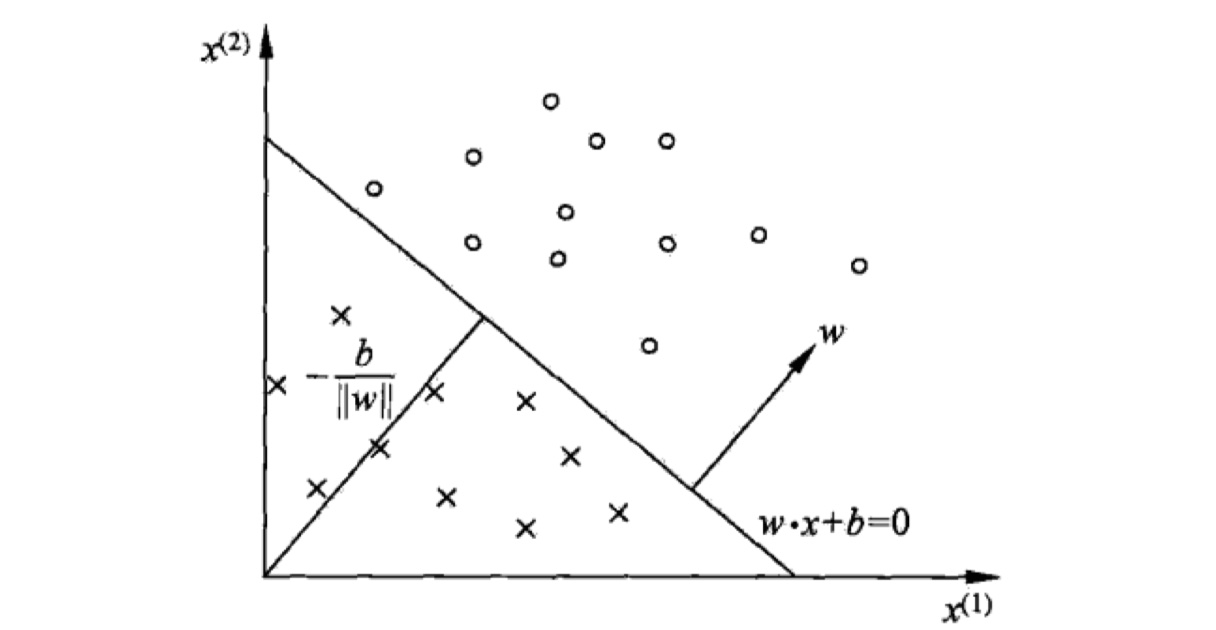
感知机模型实际上是在找一个分离超平面:$wx+b=0$,它将特征空间分成两部分。当实例类别是+1的时候,它在超平面的上方,即使得$wx+b>0$;当实例类别是-1的时候,它在超平面的下方,即使得$wx+b<0$。那么,知道了模型之后,我们发现感知机模型中有两个参数:$w,b$。那么,我们就需要找到一种学习策略来求解这两个参数,从而得到真正的感知机模型。
感知机模型的学习策略 首先,我们要知道,感知机的训练数据集是线性可分的,要不然的话,学习出来的感知机模型不会收敛。那什么是线性可分的数据集呢?如下:
给定数据集$X=\{(x_1,y_1),(x_2,y_2),(x_3,y_3),…,(x_N,y_N)\}$,其中$x_i\in R^n,y\in R,i=1…N$。如果存在某个超平面$S$,能够将$X$中的所有正例与负例能够完全区分开来,那么就说数据集$X$是线性可分的。
那么,现在给定线性可分训练数据集$X=\{(x_1,y_1),(x_2,y_2),(x_3,y_3),…,(x_N,y_N)\}$,我们要从中学习出感知机模型。我们需要考虑的是学习策略,即损失函数,也就是怎么样才能得到参数$w,b$。
对于损失函数,一个很自然的想法,就是以误分类的实例的数目为模型的损失函数。但是,这样做的一个缺陷在于,这样的损失函数不是$w,b$的可导函数,不易优化。所以,在感知机中,采取以误分类实例到分离超平面的总距离为损失函数。对于误分类点$(x_i,y_i)$,当$y_i=1$的时候,$wx_i+b<0$;当$y_i=-1$的时候,$wx_i+b>0$。那么我们将其用一个公式表达,如下:
那么,假设误分类集合为$M$,我们根据点到平面的距离公式,所有误分类点到分离超平面的总距离如下:
我们不考虑$\frac {1}{\left|w\right|}$,便得到了感知机模型的损失函数,如下:
所以,我们最小化该损失函数,就可以得到最优的参数$w,b$。此外,该损失函数是非负的,如果没有误分类点,那么损失函数为0,并且,对于一个特点的误分类点的时候,误分类点离分离超平面越近,损失函数越小。当分离超平面越过该误分类点的时候,损失函数为0。
感知机模型的学习算法 当我们定义了感知机模型的学习策略(损失函数)后,那么求解参数就变成一个最优化问题了。在这里,学习算法有其原始形式与对偶形式,下面我们将一一介绍。
感知机模型学习算法的原始形式 在感知机模型中,采取的学习算法是随机梯度下降算法(SGD)。那为什么不采取batch梯度下降呢?原因在于,只有误分类点才能被计算入损失函数中,所以不能使用所有的样本来进行优化。对于单个误分类点,我们使用损失函数对$w,b$求偏导,结果如下:
原始形式
输入:给定训练数据集$X=\{(x_1,y_1),(x_2,y_2),(x_3,y_3),…,(x_N,y_N)\}$,其中$x_i\in R^n,y\in R,i=1…N$。学习率$\eta\in (0,1]$。
输出:参数$w,b$。
初始化参数$w,b$,给定初值为$w_0,b_0$。
在训练数据集中选取实例$(x_i,y_i)$。
如果$y_i(wx_i+b)<0$,那么
转到第2步,循环,直到损失函数为0,也就是没有误分类点为止。
注意:感知机学习算法会由于选取不同的参数初值以及选取误分类点的顺序,而导致最后的模型不同,即感知机模型不唯一。
感知机模型学习算法的对偶形式 对偶形式采取的是另外一种想法,我们将参数$w,b$表示为$x_i,y_i$的线性组合,通过求解参数$w,b$的系数,从而求得参数$w,b$。具体做法是:令参数$w,b$的初值为0,这样的话,最终的$w,b$可以用如下的公式来表示:
其中,$\alpha_i=n_i\eta$,$\eta$表示学习率,$n_i$表示由于第i个实例被误分类,从而更新的次数。所以,我们只要求得$\alpha=\{\alpha_1,\alpha_2,…,\alpha_N\}$,就可以得到参数$w,b$。
对偶形式
输入:给定训练数据集$X=\{(x_1,y_1),(x_2,y_2),(x_3,y_3),…,(x_N,y_N)\}$,其中$x_i\in R^n,y\in R,i=1…N$。学习率$\eta\in (0,1]$。
输出:参数$w,b$。感知机模型$f(x)=sign(\sum_{j=1}^{N}\alpha_jy_jx_jx+b)$,其中,$\alpha=\{\alpha_1,\alpha_2,…,\alpha_N\}$。
初始化参数$w,b$,给定初值为$w_0=0,b_0=0$。
在训练数据集中选取实例$(x_i,y_i)$。
如果$y_i(\sum_{j=1}^{N}\alpha_jy_jx_jx_i+b)<0$,那么
转到第2步,直到损失函数为0,没有误分类点为止。
注意:我们如果仔细看训练过程的话,我们会发现在第3步,我们需要频繁计算训练实例的内积。那么,我们可以实现把所有实例的内积都算出来,放入一个矩阵(该矩阵叫Gram矩阵)只能够存储。当需要的时候,直接查矩阵就可以了,这样的话,就可以大大加快计算速度。这就是为什么对偶形式比原始形式更优的原因。
但是在实践中,我们并不总是选择对偶形式。当实例特征数量特别多的时候,我们选择对偶形式;当样本数量特别多的时候,我们选择原始形式。
到此,感知机的理论部分就讲完了,是不是非常简单😁?我们可以回顾一下,在感知机中,一个最重要的前提条件就是:训练数据集是线性可分的。那如果训练数据集不是线性可分的,该怎么办?这就需要大名鼎鼎的支持向量机(SVM)来进行解决了,后面就专门写一篇文章来介绍支持向量机~
感知机模型的实现 把模型实现一遍才算是真正的吃透了这个模型呀。在这里,我采取了两种方式来实现感知机模型:纯python实现以及调用scikit-learn库来实现。我的github里面可以下在到所有的代码,欢迎访问我的github,也欢迎大家star和fork。附上GitHub地址: 《统计学习方法》及常规机器学习模型实现 。具体代码如下:
纯python实现 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 ''' 数据集:Mnist数据集 模型:感知机模型,对其原始形式与对偶形式均进行了实现 实现方式:python+numpy ----------------------------------- 使用原始形式 数据量:1000(可以全部使用,主要是对偶形式做对比) 准确率:0.7691 时间:19.176676034927368 ----------------------------------- 使用对偶形式 如果使用对偶形式的话,数据集最好不要全部使用,会非常慢! (主要就是在计算gram矩阵的时候,60000✖️60000的矩阵挺大的了) 数据量:1000 准确率:0.7796. 时间:40.42902708053589 ------------------------------------ 但是如果把训练样本数目改为10的话,会发现,原始:54.4%,14.43s;对偶:65.05%,14.715s! 所以由此可以看出,当样本数远小于特征数的时候。选择对偶会更好,其余情况,选原始形式。 通过实验就看出来了~ ''' import numpy as npimport timedef loadData (fileName ): ''' 从fileName数据文件中加载Mnist数据集 :param fileName: 数据集的路径 :return: 返回数据的特征向量与标签类别 ''' data_list = [] label_list = [] with open (fileName, "r" ) as f: for line in f.readlines(): curline = line.strip().split("," ) data_list.append([int (feature) for feature in curline[1 :]]) if int (curline[0 ]) >= 5 : label_list.append(1 ) else : label_list.append(-1 ) data_matrix = np.array(data_list) label_matrix = np.array(label_list) return data_matrix, label_matrix class Perceptron (object ''' 定义Peceptron类,里面包括了其学习算法的原始形式与对偶形式的实现函数 ''' def __init__ (self, data_matrix, label_matrix, iteration=30 , learning_rate=0.0001 ): ''' 构造函数 :param data_matrix: 数据的特征向量 :param label_matrix: 数据的标签类别 :param iteration: 迭代次数,默认为100 :param learning_rate: 学习率,默认为0.001 ''' self.data_matrix = data_matrix self.label_matrix = label_matrix self.iteration = iteration self.learning_rate = learning_rate def original_method (self ): ''' 感知机学习算法的原始形式的实现 :return: 返回参数w,b ''' data_matrix = self.data_matrix label_matrix = self.label_matrix input_num, feature_num = np.shape(data_matrix) print(data_matrix.shape) w = np.random.randn(1 , feature_num) b = np.random.randn() for iter in range (self.iteration): for i in range (input_num): x_i = data_matrix[i] y_i = label_matrix[i] result = y_i * (np.matmul(w, x_i.T) + b) if result <= 0 : w = w + self.learning_rate * y_i * x_i b = b + self.learning_rate * y_i print(f"this is {iter } round ,the total round is {self.iteration} ." ) assert (w.shape == (1 , feature_num)) return w, b def dual_method (self ): ''' 感知机学习算法的对偶形式的实现 :return: ''' data_matrix = self.data_matrix label_matrix = self.label_matrix.T input_num, feature_num = np.shape(data_matrix) a = np.zeros(input_num) b = 0 print(a.shape) gram = np.matmul(data_matrix, data_matrix.T) assert (gram.shape == (input_num, input_num)) print(gram.shape) for iter in range (self.iteration): for i in range (input_num): result = 0 for j in range (input_num): result += a[j] * label_matrix[j] * gram[j][i] result += b result *= label_matrix[i] if (result <= 0 ): a[i] = a[i] + self.learning_rate b = b + self.learning_rate * label_matrix[i] else : continue print(f"this is {iter } round,the total round is {self.iteration} ." ) w = np.matmul(np.multiply(a,self.label_matrix),self.data_matrix) print(w.shape) return w, b def test_model (test_data_matrix, test_label_matrix, w, b ): ''' 再测试数据集上测试 :param test_data_matrix: 测试集的特征向量 :param test_label_matrix: 测试集的标签类别 :param w: 计算得到的参数w :param b: 计算得到的参数b :return: 返回准确率 ''' test_input_num, _ = np.shape(test_data_matrix) error_num = 0 for i in range (test_input_num): result = (test_label_matrix[i]) * (np.matmul(w, test_data_matrix[i].T) + b) if (result <= 0 ): error_num += 1 else : continue accuracy = (test_input_num - error_num) / test_input_num return accuracy if __name__ == "__main__" : start = time.time() train_data_list, train_label_list = loadData("../MnistData/mnist_train.csv" ) test_data_list, test_label_list = loadData("../MnistData/mnist_test.csv" ) print("finished load data." ) perceptron = Perceptron(train_data_list[:1000 ], train_label_list[:1000 ], iteration=30 , learning_rate=0.0001 ) w, b = perceptron.dual_method() accuracy = test_model(test_data_list, test_label_list, w, b) end = time.time() print(f"accuracy is {accuracy} ." ) print(f"the total time is {end - start} ." )
使用scikit-learn实现 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 ''' 数据集:Mnist数据集 模型:感知机模型,对其原始形式与对偶形式均进行了实现 实现方式:使用scikit-learn库 结果: 在测试集上的准确率:0.7849 时间:25,72s ''' import numpy as npimport timefrom sklearn.linear_model import Perceptrondef loadData (fileName ): ''' 从fileName数据文件中加载Mnist数据集 :param fileName: 数据集的路径 :return: 返回数据的特征向量与标签类别 ''' data_list = [] label_list = [] with open (fileName, "r" ) as f: for line in f.readlines(): curline = line.strip().split("," ) data_list.append([int (feature) for feature in curline[1 :]]) if int (curline[0 ]) >= 5 : label_list.append(1 ) else : label_list.append(-1 ) data_matrix = np.array(np.mat(data_list)) label_matrix = np.array(np.mat(label_list)) return data_matrix, label_matrix if __name__ == "__main__" : start = time.time() clf = Perceptron(n_iter_no_change=30 , eta0=0.0001 , shuffle=False ) train_data_matrix, train_label_matrix = loadData("../MnistData/mnist_train.csv" ) test_data_matrix, test_label_matrix = loadData("../MnistData/mnist_test.csv" ) print(train_data_matrix.shape) print(test_data_matrix.shape) train_label_matrix = np.squeeze(train_label_matrix) test_label_matrix = np.squeeze(test_label_matrix) print(train_label_matrix.shape) print(test_label_matrix.shape) clf.fit(train_data_matrix, train_label_matrix) accuracy = clf.score(test_data_matrix, test_label_matrix) end = time.time() print(f"accuracy is {accuracy} ." ) print(f"the total time is {end - start} ." )