NLP|文本匹配模型-DecAtt

正式开始看文本匹配的东西啦！文本匹配对NLPer来说是很重要的，不管是最后是做对话、推荐、搜索，文本匹配都是必不可少的。当然啦，BERT系列的模型出来之后，其实传统的深度学习模型效果是远远比不上的。不过这些预训练模型效果好是好，但是训练代价昂贵，当然啦，有人会说，现在已经有剪枝、量化、蒸馏这样的方法来减小预训练模型的大小，从而降低训练所需的代价(所以说模型压缩、加速这个方向还是很有前景的🤩咦，好像跑偏了，anyway)，但是这仍然远远不够，所以熟悉传统的文本匹配模型是非常有必要的。本篇博客讲解经典的DecAtt模型，并采用tensorflow2实现。

DecAtt模型介绍

DecAtt模型来源于《A Decomposable Attention Model for Natural Language Inference》论文，于2016年由google提出。主要是用于解决NLI（自然语言推理/文本蕴含）问题中。首先介绍一下什么叫NLI问题，如下：

给定一个premise A与一个hypothesis B，如果给定A的前提下，B为真，我们就说A蕴含(entailment)了B，或者说能从A推理出B；如果B为假，那么就说A与B互相矛盾(contradiction)；如果无法根据A得出B是否为真还是假，就说A与B是互相独立的(neutral)。从这个定义中，我们可以知道NLI/TE是一个三分类的问题。

DecAtt模型架构

首先，定义训练集$\{a^{(n)},b^{(n)},y^{(n)}\}_{n=1}^{N}$，其中$a^{(n)}$表示第n个样本的premise，即：$a^{(n)}=(a_3^{(n)},a_1^{(n)},a_3^{(n)},…,a_{l_a}^{(n)})$，$l_a$表示是A句子的长度，其中每一个token的维度为$d$；$b^{(n)}$表示第n个样本的hypothesis，即$b^{(n)}=(b_1^{(n)},b_2^{(n)},b_3^{(n)},…,b_{l_b}^{(n)})$，$l_b$表示是B句子的长度，其中每一个token的维度为$d$；$y^{(n)}$表示第n个样本的标签向量，即$y^{(n)}=(y_1^{(n)},y_2^{(n)},y_3^{(n)}…,y_C^{(n)})$，所以$y^{(n)}$是一个C维的one-hot向量。

DecAtt模型总共分为三部分：Attend、Compare、Aggregate。模型结构图如下：

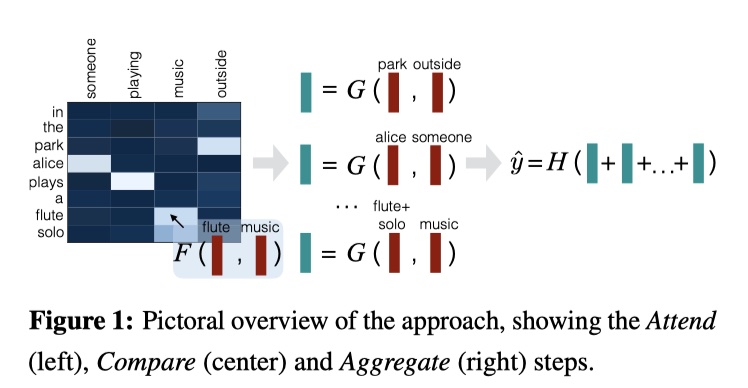
Attend

对A与B句子的token，计算它们之间的attention weights。公式如下：

$$e_{ij}=F^·(\hat a_i,\hat b_j)=F(\hat a_i)^TF(\hat b_j)$$

得到attention weights之后，我们在加权，得到新的向量，如下：

$$\beta_i=\sum_{j=1}^{l_b} \frac {e_{ij}}{\sum_{k=1}^{l_b}e_{ik}}\hat b_j \\ \alpha_j=\sum_{i=1}^{l_a} \frac {e_{ij}}{\sum_{k=1}^{l_b}e_{kj}}\hat a_i$$

需要注意的是：$\beta$与$\hat a$对齐，$\alpha$与$\hat b$对齐；另外，其中$F$表示Relu函数。为什么要这么做呢？因为如果直接使用$F^·$的话，由于$\hat a_i,\hat b_j$均是d维的向量，并且句子长度分别是$l_a,l_b$，那么，要算出全部的attention weigthts的话，要计算$l_a\times l_b$次的$F^·$计算；如果先使用relu函数先计算的话，那么就只需要$l_a+l_b$次的relu计算，大大降低了计算复杂度。这也就是为什么被称作Decomposable Attention的原因。

Compare

对加权后的一个句子与另一个原始句子相比较。

$$v_{1,i}=G([\hat a_i,\beta_i]) \\ v_{2,j}=G([\hat b_j,\alpha_j])$$

Aggregate

通过Compare，我们得到了两个向量：$\{v_{1,i}\}_{i=1}^{l_a}、\{v_{2,j}\}_{j=1}^{l_b}$，它们的维度分别是$l_a\times d、l_b\times d$。首先对两个向量集合进行求和。如下：

$$v_1=\sum_{i=1}^{l_a}v_{1,i}\\ v_2=\sum_{j=1}^{l_b}v_{2,j}$$

然后进行concatenate，输入到softmax中，得到最终的结果。

$$\hat y=H([v_1,v_2])$$

loss function采用crossentropy。

intra-sentence attention(optional)

Attend、Compare、Aggregate三步是必不可少的。除此之外，我们还可以考虑句子内token之间的相关性，从而增强句子表示，我们称作intra-sentence attention。

$$f_{ij}=F_{intra}(a_i)^TF_{intra}(b_j) \\ a_{i}^{'}=\sum_{j=1}^{l_a}\frac {exp(f_{ij}+d_{i-j})}{\sum_{k=1}^{l_a}exp(f_{ik}+d_{i-k})}a_j \\ \hat a=[a_i,a_{i}^{ '}]$$

模型训练的细节：参数初始化使用高斯分布、使用预训练的word embedding(Glove)、对于所有的relu层均适用droput(ratio=0.2)、FFN层的维度为200。

DecAtt模型实现

参考文献

A Decomposable Attention Model for Natural Language Inference