统计学习方法|最大熵模型原理详解与实现

最大熵模型(MaxEntropy)，是机器学习中一个非常重要的分类模型，其是最大熵思想应用到分类问题的结果。本篇博客将对最大熵模型的原理进行详细的讲解，并采用python实现对最大熵模型进行实现(scikit-learn库没有关于最大熵的类库)。此外，还会对比讲解其logistic回归的区别，并实现logistic回归模型(python与scikit-learn库)。

最大熵模型概述

关于使用最大熵模型，我们最终要求的是：给定实例的特征向量$x$，使得条件概率$p(y|x)$最大的$y$。但是它与朴素贝叶斯不一样，朴素贝叶斯是通过求联合概率，然后根据贝叶斯定理求得$p(y|x)$；而最大熵模型是直接求$p(y|x)$。它所使用的思想就是：最大熵思想。所谓的最大熵思想就是：当我们要求一个条件概率分布的时候，如果我们没有任何的先验知识的时候，那么我们应该选熵最大的分布；如果我们已经有了一些先验知识，那么我们应该选满足这些先验知识的情况下，熵最大的分布。下面我将介绍最大熵模型如何贯彻最大熵思想的。

最大熵模型

首先我们来看一下熵的概念，如果离散随机变量的概率分布是$P(x)$，那么它的熵如下：

$$H(P)=-\sum_xP(x)log(P(x))$$

其中，$x$表示随机变量$X$的取值。那么对于条件概率分布$P(y|x)$，它的熵，我们可以套用公式，如下：

$$H(P)=-\sum_{y}P(y|x)log(P(y|x))$$

但是这样还不够。因为我们要保证在所有情况下，熵都是最大的，所以需要引入$\tilde P(x)$。如下：

$$H(P)=-\sum_{x,y}\tilde P(x)P(y|x)log(P(y|x))$$

关于$\tilde P(x)$，我们可以这么理解：由于我们要求的是最大熵，也就是说，在满足先验知识的基础上，总的熵是最大的。由于对于每一个$x$，都会对应一个概率分布$P(y|x)$，也就会对应一个熵。所以，最大化熵，也就是最大化这些所有的熵的和。此外，我们还需要体现出每一个概率分布的熵的重要性，我们需要对其进行加权求和，$\tilde P(x)$就相当于权重。

接下来，我们还需要定义一些约束条件。因为训练集就相当于是先验知识，最大熵就是满足先验知识的基础上的熵最大的条件概率分布。我们定义特征函数$f_i(x,y)$，如下：

$$f_i(x,y)=\begin{cases} 1&,\ x与y满足某一事实 \\ 0&,\ 否则 \end{cases}$$

其中$i$表示第$i$个特征，$i=1,2,3,…,n$。那么$f(x,y)$关于$\tilde P(x,y)$的期望如下：

$$E_{\tilde P}=\sum_{x,y}\tilde P(x,y)f(x,y)=\sum_{x,y}\tilde P(x)\tilde P(y|x)f(x,y)$$

如果说我们的模型正确的话，那么$P(y|x)=\tilde P(y|x)$。所以这就是一种约束，约束我们必须要去得到正确的模型！

最大熵模型总结如下：

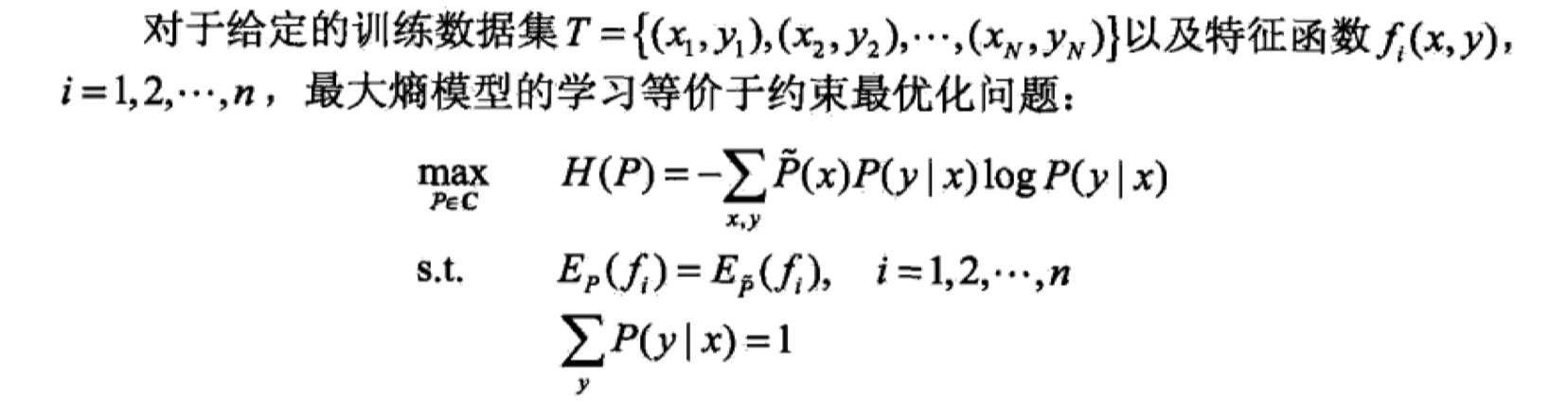
由于我们习惯最小化问题，所以：

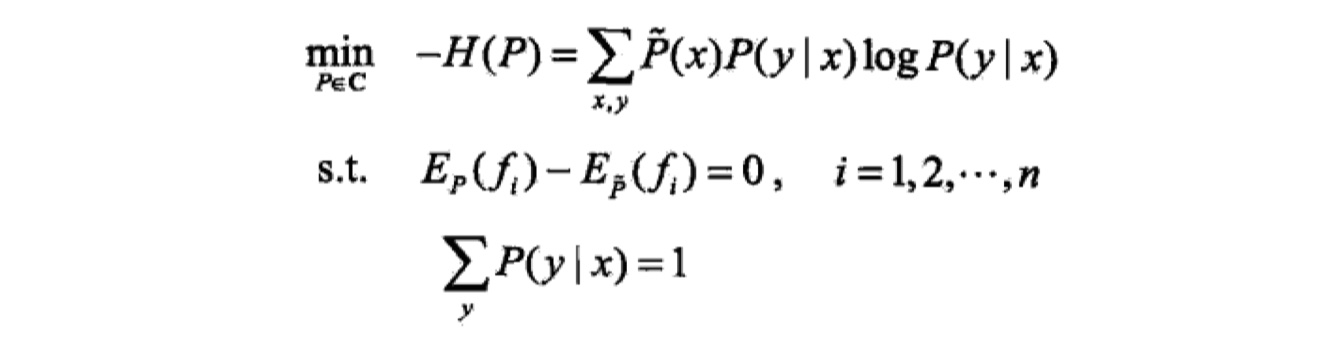
最大熵模型的学习

我们首先将最大熵模型摘抄下来：

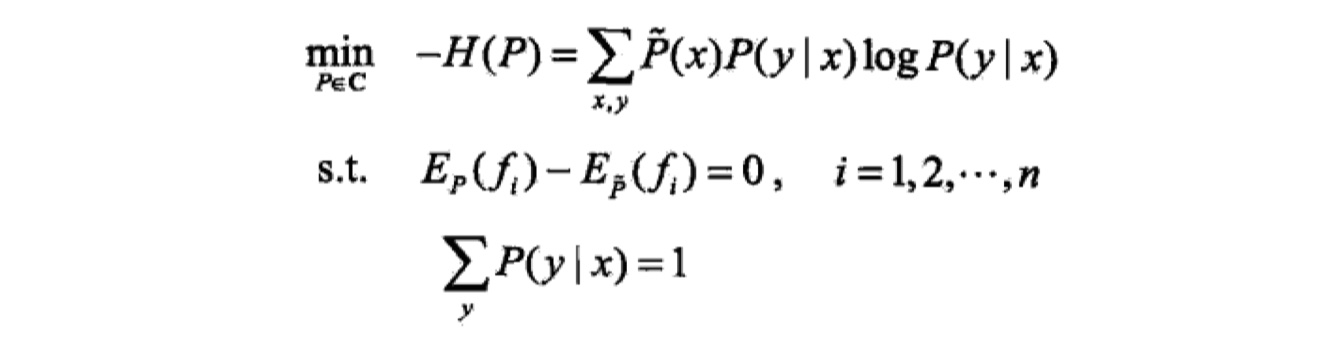
那么，对于有约束的最优化问题，很自然地就想到拉格朗日乘子法，所以我们可以写成如下形式：

所以，对于原始问题，我们的目标是：$min_Pmax_wL(P,w)$；对于对偶问题，我们的目标就是：$max_wmin_PL(P,w)$。我们首先求$min_PL(P,w)$，也就是求$\frac {\partial L}{\partial P}=0$，假设我们得到的最优解记为：$P_w(y|x)$，最后结果是：

在求得了$P_w(y|x)$之后，我们就只需要求$max_w(P_w,w)$即可。将$P_w$ 带入到原来的拉格朗日函数，化简，然后求导，即：$\frac {\partial L(P_w,w)}{\partial w}=0$。但是我们会发现，化简后太难求了，所以我们就采用另外一种方式，就是将对偶函数的最大化转化为最大熵模型的极大似然估计。下面是推导出最大熵模型的极大似然估计过程(《统计学习方法》中并没有给出推导过程)：

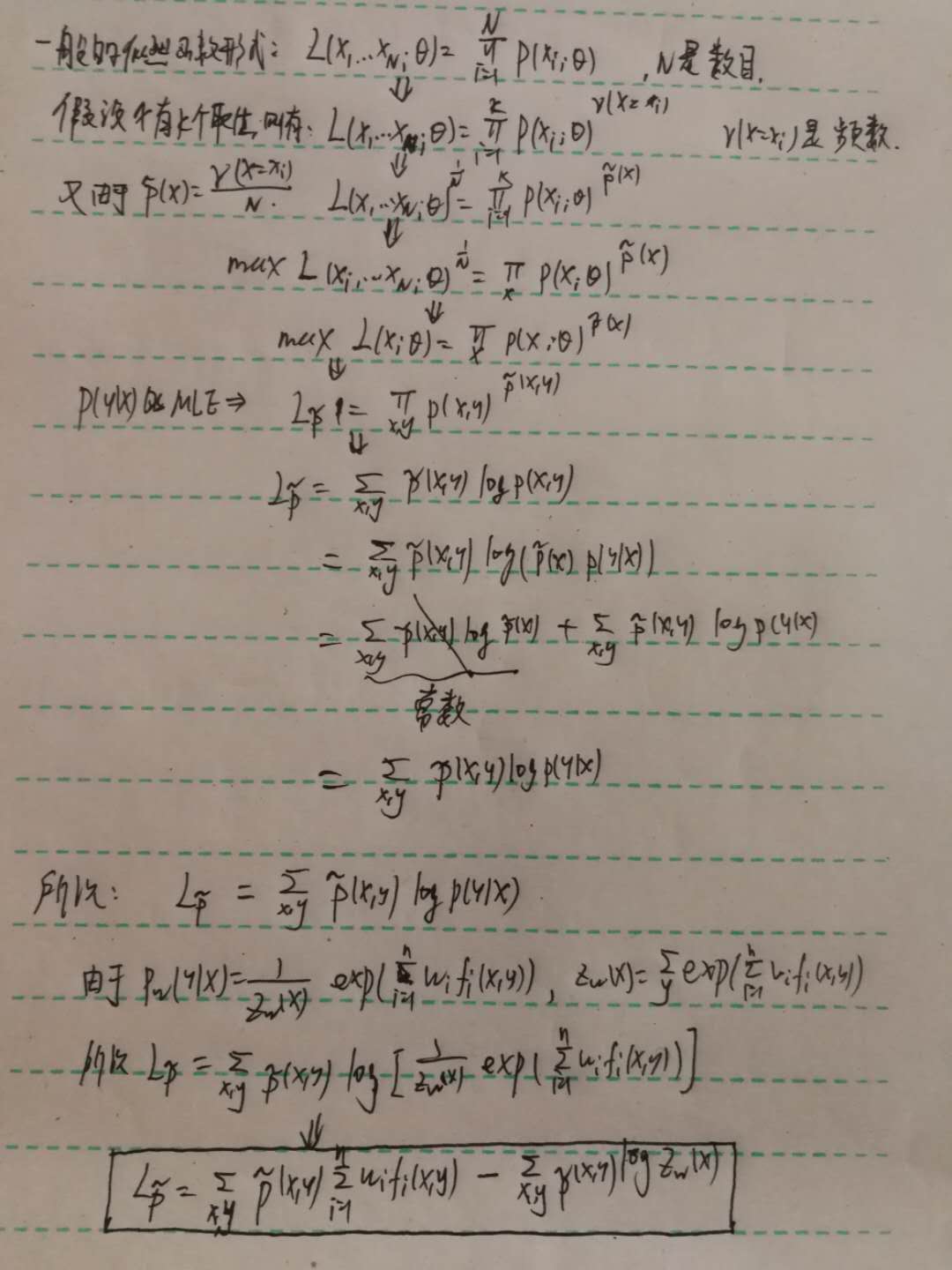
此外，可以证明化简后的对偶问题与最大熵模型的对数似然函数是一样的，感兴趣的读者可以自行证明一下。

最大熵模型学习的优化算法

现在，我们整理一下，我们已经得到的东西：最大熵模型、模型的对数似然函数。那么，接下来，我们只要对对数似然函数求导，得出参数$w$的值，就可以得到最大熵模型$P_w(y|x)$。由于最大化对数似然函数是一个凸优化问题，我们可以使用牛顿法、IIS等算法求解。在这里主要介绍IIS（改进的迭代程度法）。

IIS的思想是：如果我们能找到一种参数更新方法：$r:w->w+\delta$，使得对数似然函数能够增大，那么，我们就可以重复使用改方法，从而得到最优解。我们可以首先计算似然函数的改变量：

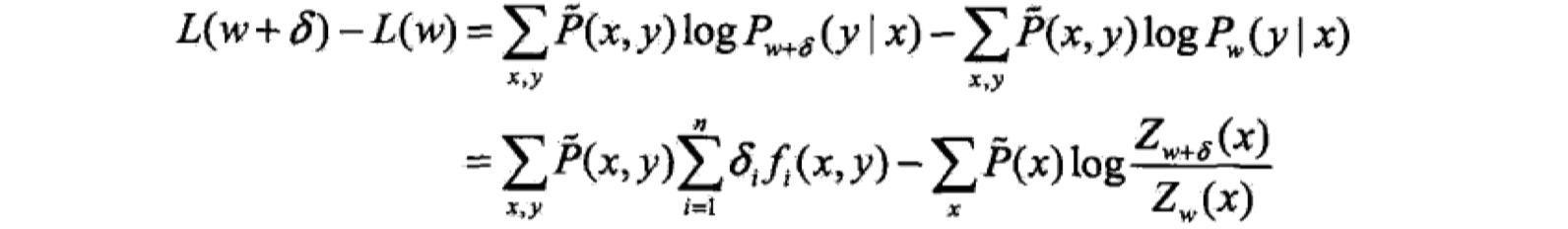
根据不等式：$-loga>=1-a$，那么将上式进行放缩，得到如下式子：

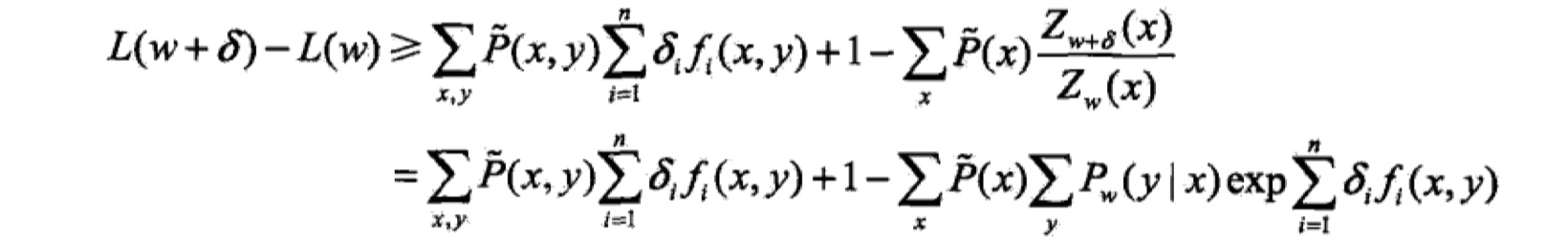
我们记右边的式子为：$A(\delta|w)$。这就是似然函数改变量的下界。也就是说，只要我们找到合适的$\delta$，不断提高下界，就能够使得似然函数不断增大。但是IIS算法一次只能优化一个参数$w_i$，所以我们需要再对下界进行放缩（这其中用到了Jensen不等式）。如下：

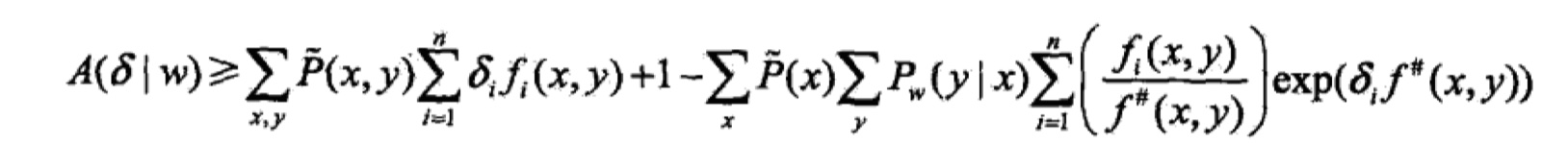
记右边的式子为$B(\delta|w)$，接下来我们只要对$B(\delta|w$求导，就可以得到最后的结果了。总结如下：

到此，最大熵模型的理论部分求讲解完了～

最大熵模型与LR模型的区别与联系

由于最大熵模型与LR模型总是被放在一起讲，所以这里就简单概括一下两者的区别与联系。最大熵模型与logistic回归模型最大的相似之处在于：最后都是求条件概率分布关于训练集的对数似然函数的最大化，区别在于：条件概率分布的形式不同，LR模型的条件概率分布就是sigmoid函数。具体关于LR模型的细节，我就不讲了，因为实在太简单了，我就放一张LR模型的对数似然函数的最大化的推导过程吧～

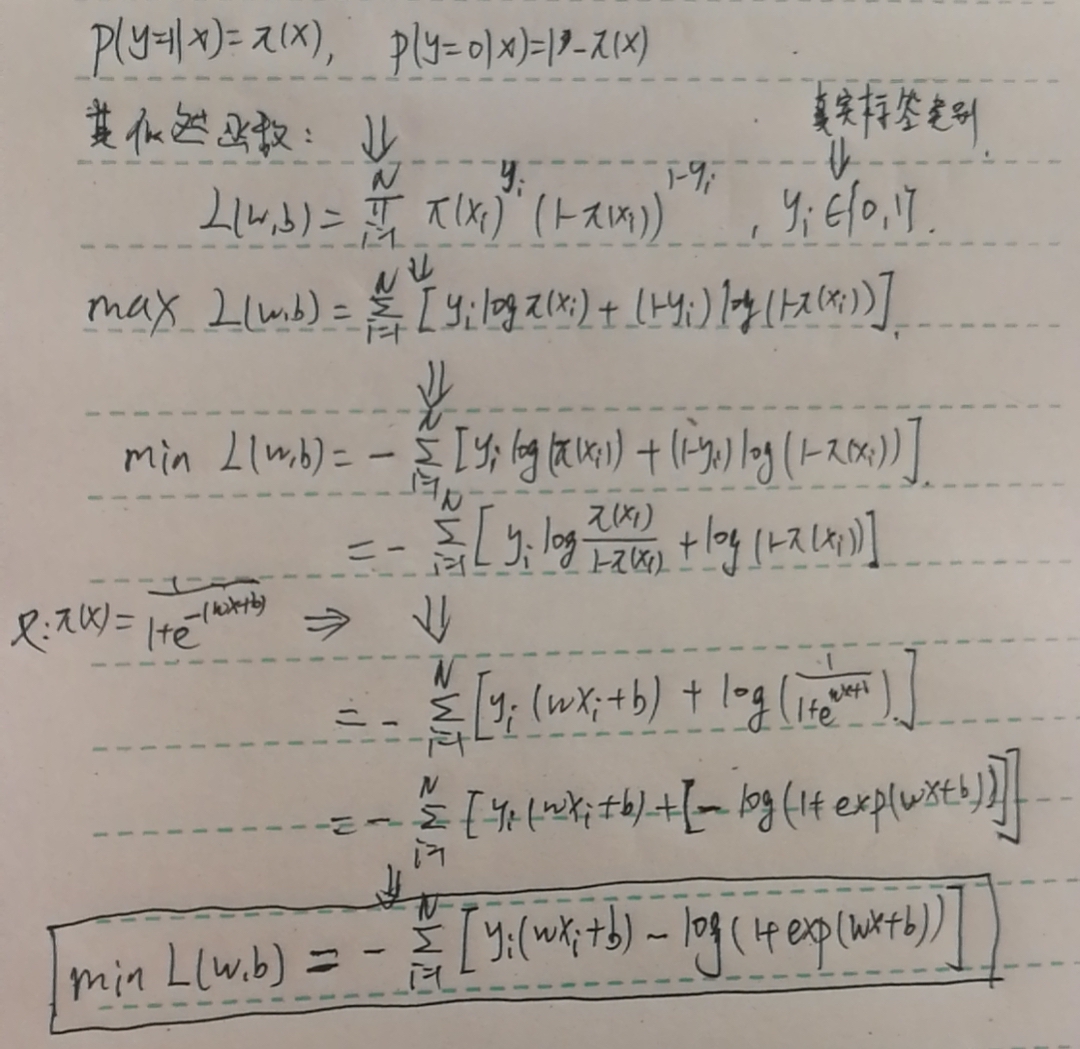
最大熵模型的实现

把模型实现一遍才算是真正的吃透了这个模型呀。在这里，我采取了python来实现最大熵模型与logistic回归模型。我的github里面可以下在到所有的代码，欢迎访问我的github，也欢迎大家star和fork。附上GitHub地址: 《统计学习方法》及常规机器学习模型实现。具体代码如下：

logistic回归模型python实现

# coding:utf-8
# Author:codewithzichao
# Date:2020-1-2
# E-mail:lizichao@pku.edu.cn

'''
数据集：Mnist
准确率：0.9919
时间：29.48268699645996
--------------
tips:在加载数据的时候，把>=5为1，<5为0这样处理数据的时候，在同样的训练次数与学习率的时候，最后的准确率只有78%左右。
可能是数据类别太多，导致比较混乱，所以在这里，我采取的是标签为0的为1，不为0的全为0。
这样准确率大大提高了。
--------------
注意，这里实现的LR模型采用的是神经网络的思想，就是将LR模型视为一个单层神经网络。按照前向传播与反向传播的方式来写的代码。
'''

import numpy as np
import time


def loadData(fileName):
    '''
    加载数据
    :param fileName:数据路径名
    :return: 特征向量矩阵、还有标签矩阵
    '''
    data_list = [];
    label_list = []

    with open(fileName, "r") as f:
        for line in f.readlines():
            curline = line.strip().split(",")
            if (int(curline[0]) ==0):
                label_list.append(1)
            else:
                label_list.append(0)
            data_list.append([int(feature) / 255 for feature in curline[1:]])

    data_matrix = np.array(data_list)
    label_matrix = np.array(label_list).reshape(1, -1)
    return data_matrix, label_matrix


def sigmoid(z):
    '''
    定义sigmoid函数
    :param z: 输入
    :return: 返回（0，1）的数
    '''
    result = 1 / (1 + np.exp(-z))
    return result


def initialize_params(feature_dim):
    '''
    初始化参数w,b
    :param feature_dim:实例特征数目
    :return: 参数w,b
    '''
    w = np.zeros((feature_dim, 1))
    b = 0

    return w, b


def propagation(w, b, X, Y):
    '''
    一次前向与反向传播过程
    :param w:参数w
    :param b: 参数b
    :param X: 输入的特征向量
    :param Y: 输入的类别向量
    :return:dw,db,costs
    '''
    N, _ = np.shape(X)  # 训练集数目
    X = X.T
    # print(X.shape)
    A = sigmoid(np.dot(w.T, X) + b)
    # epsilon=1e-5
    cost = -1 / N * (np.sum(Y * np.log(A) + (1 - Y) * np.log(1 - A)))

    dz = A - Y
    dw = 1 / N * np.dot(X, dz.T)
    db = 1 / N * np.sum(dz)

    assert (dw.shape == w.shape)
    assert (db.dtype == float)

    cost = np.squeeze(cost)
    assert (cost.shape == ())

    grads = {"dw": dw, "db": db}

    return grads, cost


def optimization(w, b, X, Y, iterations, learning_rate):
    '''
    优化，使用batch GD
    :param w: 参数w
    :param b: 参数b
    :param X: 输入的特征向量
    :param Y: 输入的类别向量
    :param iterations: 迭代次数(其实就是epoch)
    :param learning_rate: 学习率
    :return: 最优化的参数w,b,以及costs（costs可有可无，取决于你是否想看训练过程中的cost的变化）
    '''
    costs = []

    for iter in range(iterations):
        grads, cost = propagation(w, b, X, Y)

        dw = grads["dw"]
        db = grads["db"]

        w = w - learning_rate * dw
        b = b - learning_rate * db

        # 每100次epoch打印一次信息
        if (iter % 100 == 0):
            costs.append(cost)
            print(f"the current iteration is {iter},the current cost is {cost}.")

        params = {"w": w, "b": b}
        grads = {"dw": dw, "db": db}

    return params, grads, costs


def predict(w, b, X):
    '''
    预测新实例的类别
    :param w:最优化的参数w
    :param b:最优化的参数b
    :param X:实例的特征向量
    :return:实例的类别
    '''
    N = X.shape[0]
    prediction = np.zeros((1, N))
    X = X.T
    A = sigmoid(np.dot(w.T, X) + b)

    for i in range(N):
        if (A[0][i] <= 0.5):
            prediction[0][i] = 0
        else:
            prediction[0][i] = 1

    assert (prediction.shape == (1, N))

    return prediction


def model(train_data, train_label, test_data, test_label, iterations, learning_rate):
    '''
    将上述定义的函数结合起来，就是整个LR模型的执行过程
    :param train_data: 训练数据集
    :param train_label: 训练数据集的标签
    :param test_data: 测试数据集
    :param test_label: 测试数据集的标签
    :param iterations: 迭代次数(epoch)
    :param learning_rate: 学习率
    :return: 在测试数据集上的准确率
    '''
    w, b = initialize_params(train_data.shape[1])
    params, grads, costs = optimization(w, b, train_data, train_label, iterations, learning_rate)

    w = params["w"]
    b = params["b"]

    prediction = predict(w, b, test_data)
    error = 0
    for i in range(prediction.shape[1]):
        if (prediction[0][i] != test_label[0][i]):
            error += 1

    accuracy = (prediction.shape[1] - error) / prediction.shape[1]

    print(f"the accuracy is {accuracy}.")

    d = {"w": w, "b": b, "costs": costs}
    return d


if __name__ == "__main__":
    start = time.time()

    print("start load data.")
    train_data, train_label = loadData("../MnistData/mnist_train.csv")
    test_data, test_label = loadData("../MnistData/mnist_test.csv")
    print("finished load data.")

    d = model(train_data, train_label, test_data, test_label, iterations=200, learning_rate=0.7)

    end = time.time()
    print(f"the total time is {end - start}.")

logistic回归模型sckit-learn实现

# coding:utf-8
# Author:codewithzichao
# Date:2020-1-2
# E-mail:lizichao@pku.edu.cn

'''
数据集：Mnist
准确率：0.8707.
时间：89.82440423965454.
'''

import numpy as np
import time

from sklearn import linear_model
from sklearn.model_selection import train_test_split


def loadData(fileName):
    '''
    加载数据
    :param fileName:数据路径名
    :return: 特征向量矩阵、还有标签矩阵
    '''
    data_list = []
    label_list = []

    with open(fileName, "r") as f:
        for line in f.readlines():
            curline = line.strip().split(",")
            if (int(curline[0]) >= 5):
                label_list.append(1)
            else:
                label_list.append(0)
            data_list.append([int(feature) / 255 for feature in curline[1:]])

    data_matrix = np.array(data_list)
    label_matrix = np.array(label_list)
    return data_matrix, label_matrix


if __name__ == "__main__":
    start = time.time()

    print("start load data.")
    train_data, train_label = loadData("../Mnistdata/mnist_train.csv")
    test_data, test_label = loadData("../MnistData/mnist_test.csv")
    print("finished load data.")

    # 默认迭代次数为100,使用的算法是lbfgs，使用L2正则化。这里要加大迭代次数，要不然的化，不会收敛。
    clf = linear_model.LogisticRegression(max_iter=1000)
    clf.fit(train_data, train_label)

    accuracy = clf.score(test_data, test_label)
    print(f"the  accuracy is {accuracy}.")

    end = time.time()
    print(f"the total time is {end - start}.")

最大熵模型的实现

此实现借用于pkudodo的实现，因为实在是写的太好了！

#coding:utf-8
#Author:codewithzichao
#Date:2020-1-2
#E-mail:lizichao@pku.edu.cn

import numpy as np
import time
from collections import defaultdict

'''
数据集：Mnist
训练集数量：60000(实际使用:20000)
测试集数量：10000
'''

def loadData(fileName):
    '''
    加载数据
    :param fileName:数据路径名
    :return: 特征向量矩阵、还有标签矩阵
    '''
    data_list = [];label_list = []

    with open(fileName, "r") as f:
        for line in f.readlines():
            curline = line.strip().split(",")
            if (int(curline[0]) >= 5):
                label_list.append(1)
            else:
                label_list.append(0)
            data_list.append([int(int(feature)>128)  for feature in curline[1:]])

    data_matrix = np.array(data_list)
    label_matrix = np.array(label_list)
    return data_matrix, label_matrix


class maxEnt:
    '''
    最大熵类
    '''
    def __init__(self, trainDataList, trainLabelList, testDataList, testLabelList):
        '''
        各参数初始化
        '''
        self.trainDataList = trainDataList          #训练数据集
        self.trainLabelList = trainLabelList        #训练标签集
        self.testDataList = testDataList            #测试数据集
        self.testLabelList = testLabelList          #测试标签集
        self.featureNum = len(trainDataList[0])     #特征数量

        self.N = len(trainDataList)                 #总训练集长度
        self.n = 0                                  #训练集中（xi，y）对数量
        self.M = 10000                              #
        self.fixy = self.calc_fixy()                #所有(x, y)对出现的次数
        self.w = [0] * self.n                       #Pw(y|x)中的w
        self.xy2idDict, self.id2xyDict = self.createSearchDict()        #(x, y)->id和id->(x, y)的搜索字典
        self.Ep_xy = self.calcEp_xy()               #Ep_xy期望值

    def calcEpxy(self):
        '''
        计算特征函数f(x, y)关于模型P(Y|X)与经验分布P_(X, Y)的期望值（P后带下划线“_”表示P上方的横线
        程序中部分下划线表示“|”，部分表示上方横线，请根据具体公式自行判断,）
        即“6.2.2 最大熵模型的定义”中第二个期望（83页最上方的期望）
        :return:
        '''
        Epxy = [0] * self.n
        #对于每一个样本进行遍历
        for i in range(self.N):
            #初始化公式中的P(y|x)列表
            Pwxy = [0] * 2
            #计算P(y = 0 } X)
            #注：程序中X表示是一个样本的全部特征，x表示单个特征，这里是全部特征的一个样本
            Pwxy[0] = self.calcPwy_x(self.trainDataList[i], 0)
            #计算P(y = 1 } X)
            Pwxy[1] = self.calcPwy_x(self.trainDataList[i], 1)

            for feature in range(self.featureNum):
                for y in range(2):
                    if (self.trainDataList[i][feature], y) in self.fixy[feature]:
                        id = self.xy2idDict[feature][(self.trainDataList[i][feature], y)]
                        Epxy[id] += (1 / self.N) * Pwxy[y]
        return Epxy

    def calcEp_xy(self):
        '''
        计算特征函数f(x, y)关于经验分布P_(x, y)的期望值（下划线表示P上方的横线，
        同理Ep_xy中的“_”也表示p上方的横线）
        即“6.2.2 最大熵的定义”中第一个期望（82页最下方那个式子）
        :return: 计算得到的Ep_xy
        '''
        #初始化Ep_xy列表，长度为n
        Ep_xy = [0] * self.n

        #遍历每一个特征
        for feature in range(self.featureNum):
            #遍历每个特征中的(x, y)对
            for (x, y) in self.fixy[feature]:
                #获得其id
                id = self.xy2idDict[feature][(x, y)]
                #将计算得到的Ep_xy写入对应的位置中
                #fixy中存放所有对在训练集中出现过的次数，处于训练集总长度N就是概率了
                Ep_xy[id] = self.fixy[feature][(x, y)] / self.N

        #返回期望
        return Ep_xy

    def createSearchDict(self):
        '''
        创建查询字典
        xy2idDict：通过(x,y)对找到其id,所有出现过的xy对都有一个id
        id2xyDict：通过id找到对应的(x,y)对
        '''
        #设置xy搜多id字典
        #这里的x指的是单个的特征，而不是某个样本，因此将特征存入字典时也需要存入这是第几个特征
        #这一信息，这是为了后续的方便，否则会乱套。
        #比如说一个样本X = (0, 1, 1) label =(1)
        #生成的标签对有(0, 1), (1, 1), (1, 1)，三个(x，y)对并不能判断属于哪个特征的，后续就没法往下写
        #不可能通过(1, 1)就能找到对应的id，因为对于(1, 1),字典中有多重映射
        #所以在生成字典的时总共生成了特征数个字典，例如在mnist中样本有784维特征，所以生成784个字典，属于
        #不同特征的xy存入不同特征内的字典中，使其不会混淆
        xy2idDict = [{} for i in range(self.featureNum)]
        #初始化id到xy对的字典。因为id与(x，y)的指向是唯一的，所以可以使用一个字典
        id2xyDict = {}

        #设置缩影，其实就是最后的id
        index = 0
        #对特征进行遍历
        for feature in range(self.featureNum):
            #对出现过的每一个(x, y)对进行遍历
            #fixy：内部存放特征数目个字典，对于遍历的每一个特征，单独读取对应字典内的(x, y)对
            for (x, y) in self.fixy[feature]:
                #将该(x, y)对存入字典中，要注意存入时通过[feature]指定了存入哪个特征内部的字典
                #同时将index作为该对的id号
                xy2idDict[feature][(x, y)] = index
                #同时在id->xy字典中写入id号，val为(x, y)对
                id2xyDict[index] = (x, y)
                #id加一
                index += 1

        #返回创建的两个字典
        return xy2idDict, id2xyDict


    def calc_fixy(self):
        '''
        计算(x, y)在训练集中出现过的次数
        :return:
        '''
        #建立特征数目个字典，属于不同特征的(x, y)对存入不同的字典中，保证不被混淆
        fixyDict = [defaultdict(int) for i in range(self.featureNum)]
        #遍历训练集中所有样本
        for i in range(len(self.trainDataList)):
            #遍历样本中所有特征
            for j in range(self.featureNum):
                #将出现过的(x, y)对放入字典中并计数值加1
                fixyDict[j][(self.trainDataList[i][j], self.trainLabelList[i])] += 1
        #对整个大字典进行计数，判断去重后还有多少(x, y)对，写入n
        for i in fixyDict:
            self.n += len(i)
        #返回大字典
        return fixyDict


    def calcPwy_x(self, X, y):
        '''
        计算“6.23 最大熵模型的学习” 式6.22
        :param X: 要计算的样本X（一个包含全部特征的样本）
        :param y: 该样本的标签
        :return: 计算得到的Pw(Y|X)
        '''
        #分子
        numerator = 0
        #分母
        Z = 0
        #对每个特征进行遍历
        for i in range(self.featureNum):
            #如果该(xi,y)对在训练集中出现过
            if (X[i], y) in self.xy2idDict[i]:
                #在xy->id字典中指定当前特征i，以及(x, y)对：(X[i], y)，读取其id
                index = self.xy2idDict[i][(X[i], y)]
                #分子是wi和fi(x，y)的连乘再求和，最后指数
                #由于当(x, y)存在时fi(x，y)为1，因为xy对肯定存在，所以直接就是1
                #对于分子来说，就是n个wi累加，最后再指数就可以了
                #因为有n个w，所以通过id将w与xy绑定，前文的两个搜索字典中的id就是用在这里
                numerator += self.w[index]
            #同时计算其他一种标签y时候的分子，下面的z并不是全部的分母，再加上上式的分子以后
            #才是完整的分母，即z = z + numerator
            if (X[i], 1-y) in self.xy2idDict[i]:
                #原理与上式相同
                index = self.xy2idDict[i][(X[i], 1-y)]
                Z += self.w[index]
        #计算分子的指数
        numerator = np.exp(numerator)
        #计算分母的z
        Z = np.exp(Z) + numerator
        #返回Pw(y|x)
        return numerator / Z


    def maxEntropyTrain(self, iter = 500):
        #设置迭代次数寻找最优解
        for i in range(iter):
            #单次迭代起始时间点
            iterStart = time.time()

            #计算“6.2.3 最大熵模型的学习”中的第二个期望（83页最上方哪个）
            Epxy = self.calcEpxy()

            #使用的是IIS，所以设置sigma列表
            sigmaList = [0] * self.n
            #对于所有的n进行一次遍历
            for j in range(self.n):
                #依据“6.3.1 改进的迭代尺度法” 式6.34计算
                sigmaList[j] = (1 / self.M) * np.log(self.Ep_xy[j] / Epxy[j])

            #按照算法6.1步骤二中的（b）更新w
            self.w = [self.w[i] + sigmaList[i] for i in range(self.n)]

            #单次迭代结束
            iterEnd = time.time()
            #打印运行时长信息
            print('iter:%d:%d, time:%d'%(i, iter, iterStart - iterEnd))

    def predict(self, X):
        '''
        预测标签
        :param X:要预测的样本
        :return: 预测值
        '''
        #因为y只有0和1，所有建立两个长度的概率列表
        result = [0] * 2
        #循环计算两个概率
        for i in range(2):
            #计算样本x的标签为i的概率
            result[i] = self.calcPwy_x(X, i)
        #返回标签
        #max(result)：找到result中最大的那个概率值
        #result.index(max(result))：通过最大的那个概率值再找到其索引，索引是0就返回0，1就返回1
        return result.index(max(result))

    def test(self):
        '''
        对测试集进行测试
        :return:
        '''
        #错误值计数
        errorCnt = 0
        #对测试集中所有样本进行遍历
        for i in range(len(self.testDataList)):
            #预测该样本对应的标签
            result = self.predict(self.testDataList[i])
            #如果错误，计数值加1
            if result != self.testLabelList[i]:   errorCnt += 1
        #返回准确率
        return 1 - errorCnt / len(self.testDataList)

if __name__ == '__main__':
    start = time.time()

    # 获取训练集及标签
    print('start read transSet')
    trainData, trainLabel = loadData('../Mnist/mnist_train.csv')

    # 获取测试集及标签
    print('start read testSet')
    testData, testLabel = loadData('../Mnist/mnist_test.csv')

    #初始化最大熵类
    maxEnt = maxEnt(trainData[:20000], trainLabel[:20000], testData, testLabel)

    maxEnt.maxEntropyTrain()

    accuracy = maxEnt.test()
    print(f"the accuracy is {accuracy}.")

    # 打印时间
    print('time span:', time.time() - start)