到目前为止,已经学了很多东西,但是没有输出,总感觉似乎少了点什么。这篇博客将回顾经典的LSTM与GRU。LSTM与GRU是RNN中最为经典的unit,它的提出解决了RNN中梯度消失的问题,非常地具有开创性。本文将具体探究其原理细节。
本文的符号体系借鉴andrew Ng的《deep learning》课程。
为什么要有LSTM?
首先我们来回顾一下基本的RNN网络架构:
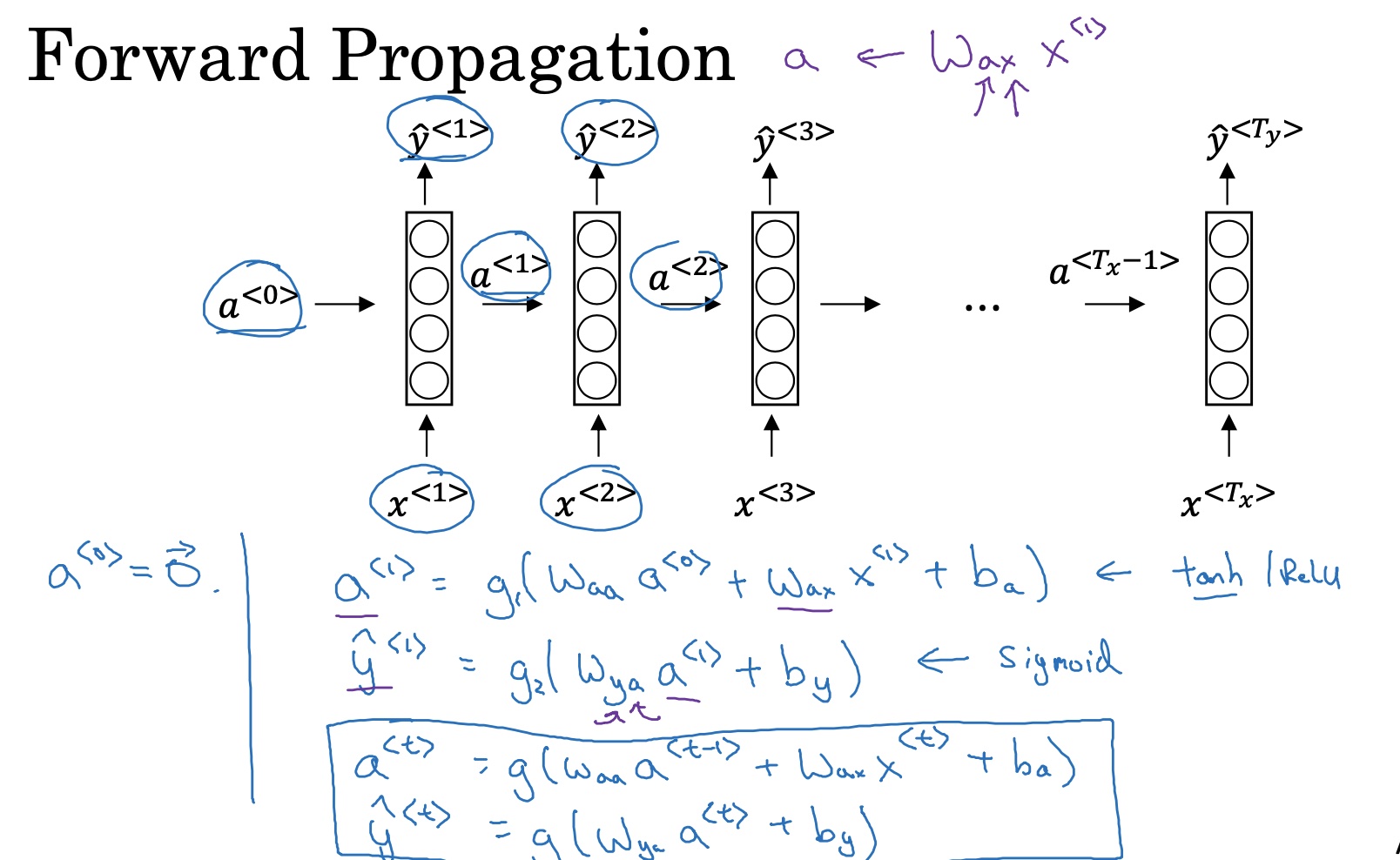
前向传播过程:
t时刻的激活值与输出值的计算公式如下:
注意:同一层,所有的$W_a$参数都是共享的,所有的$W_y$参数都是共享的,所有的$b_a$参数都是共享的,所有的$b_y$参数都是共享的。
反向传播过程(BPTT):
确定优化参数:$W_a$、$W_y$、$b_a$、$b_y$。
接下来需要定义loss function,以二分类问题为例,使用后交叉熵,则计算公式如下:
之后不断使用SGD/mini-batch GD或者其他的优化算法,优化参数:$W_a$、$W_y$、$b_a$、$b_y$,便可完成整个反向传播过程。
梯度消失
但是RNN与传统的神经网络一样,如果随着序列长度的增加,会存在梯度消失问题。原因在于:当我们对进行反向传播的时候,譬如我们计算$W_a$,我们会得到这个式子:$W_a=\prod_{t=1}^{T_x}{tanh}’W_a$。由于tanh函数的导数在(0,1)之间,如果在反向传播的时候,当参数$W_a$初始化为小于1的数,那么偏导相乘的结果就会远远小于1,从而导致梯度消失。但是由于RNN中梯度相加,所以梯度永远不会等于0。参看链接:RNN梯度消失的原因
由于RNN梯度消失的问题,就会导致梯度被近距离主导,从而导致模型难以学到远距离的依赖关系(长时期依赖问题)。这也就是为什么LSTM被提出的原因,因为LSTM能够很好地解决这一问题。
LSTM原理剖析
LSTM,全称long-short term memory networks。LSTM的设计就是为了避免上节所说的长时期依赖问题,能够记住很长时间内地信息。
RNN与LSTM内部结构
RNN内部结构如下。
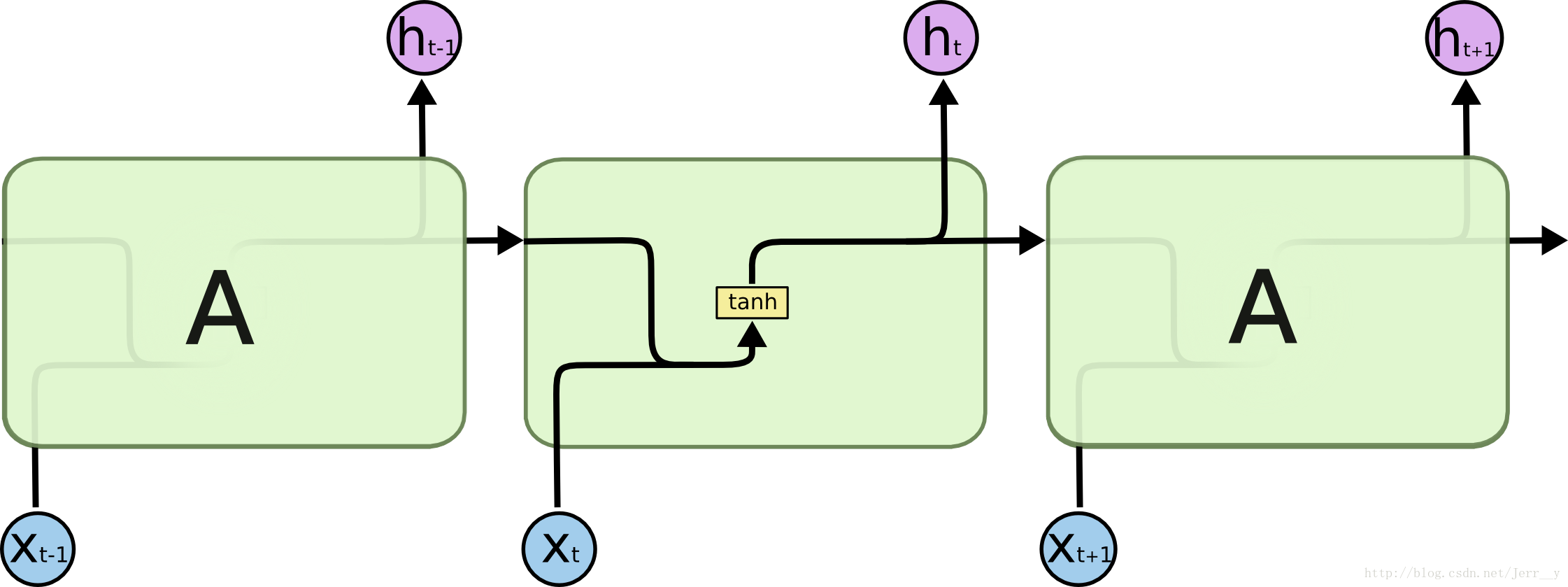
LSTM内部结构如下。
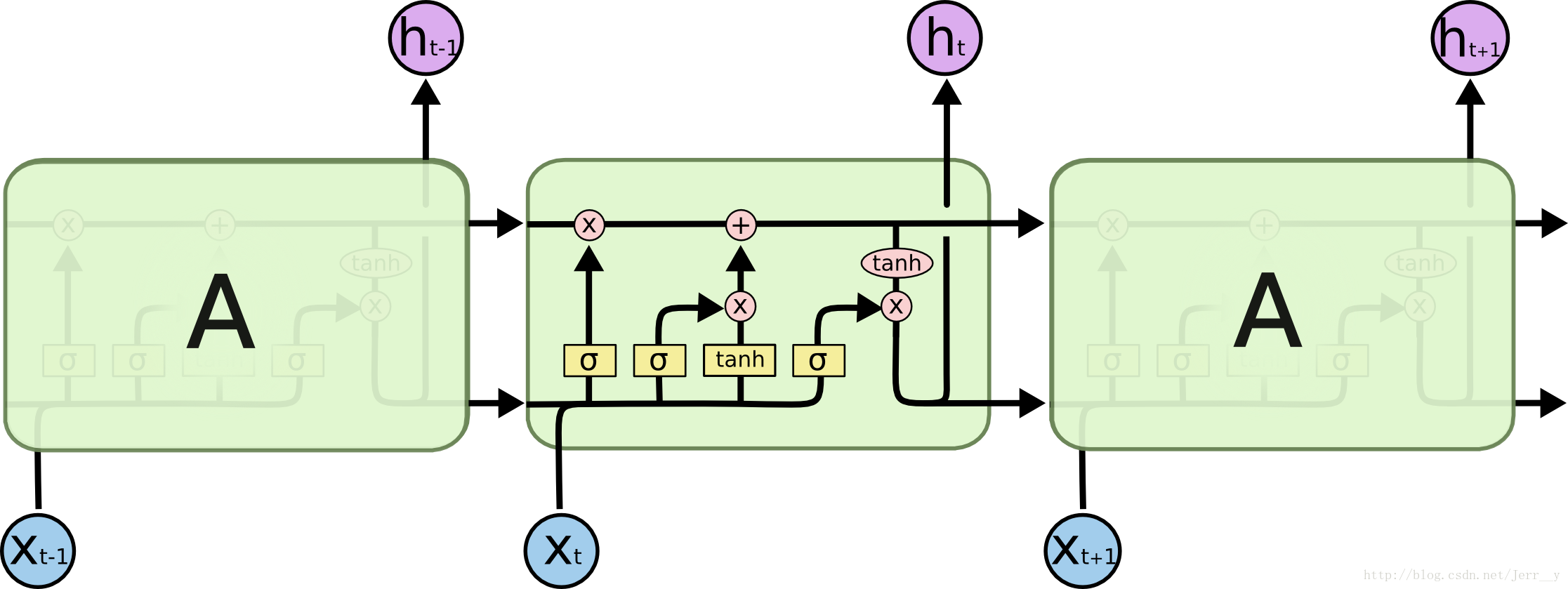
LSTM内部结构剖析
遗忘门
遗忘门决定要保留哪些信息继续通过当前的cell。$f_t$通过sigmoid函数实现,从而将$f_t$限制在(0,1)之间。0表示不让任何信息通过,1表示让所有信息通过。
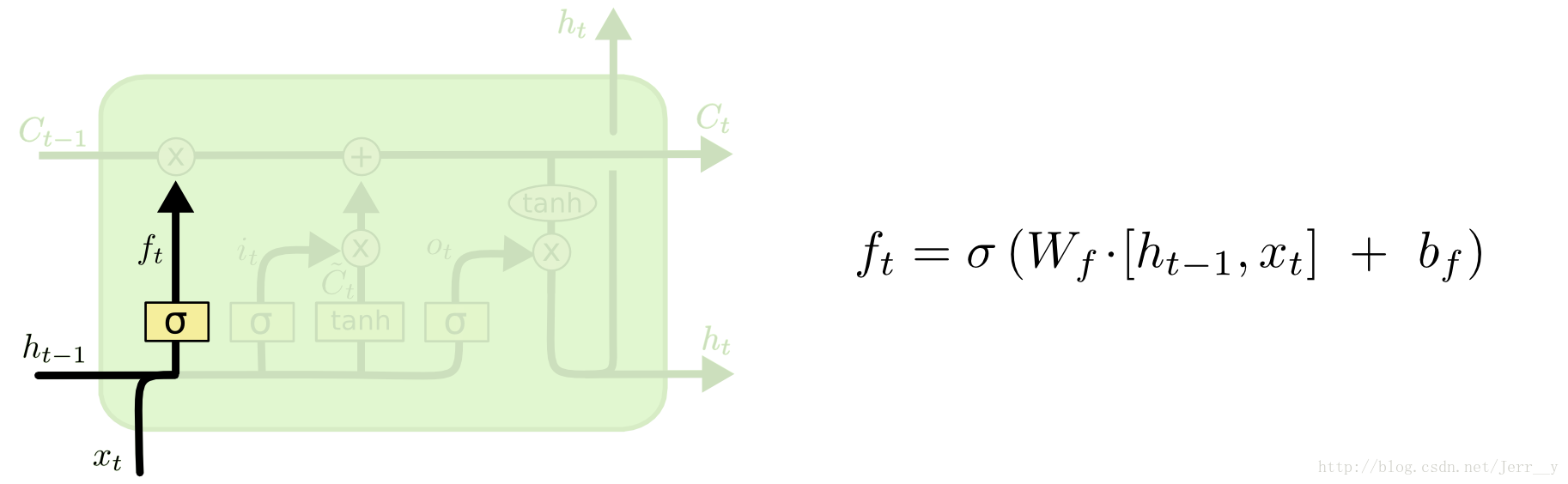
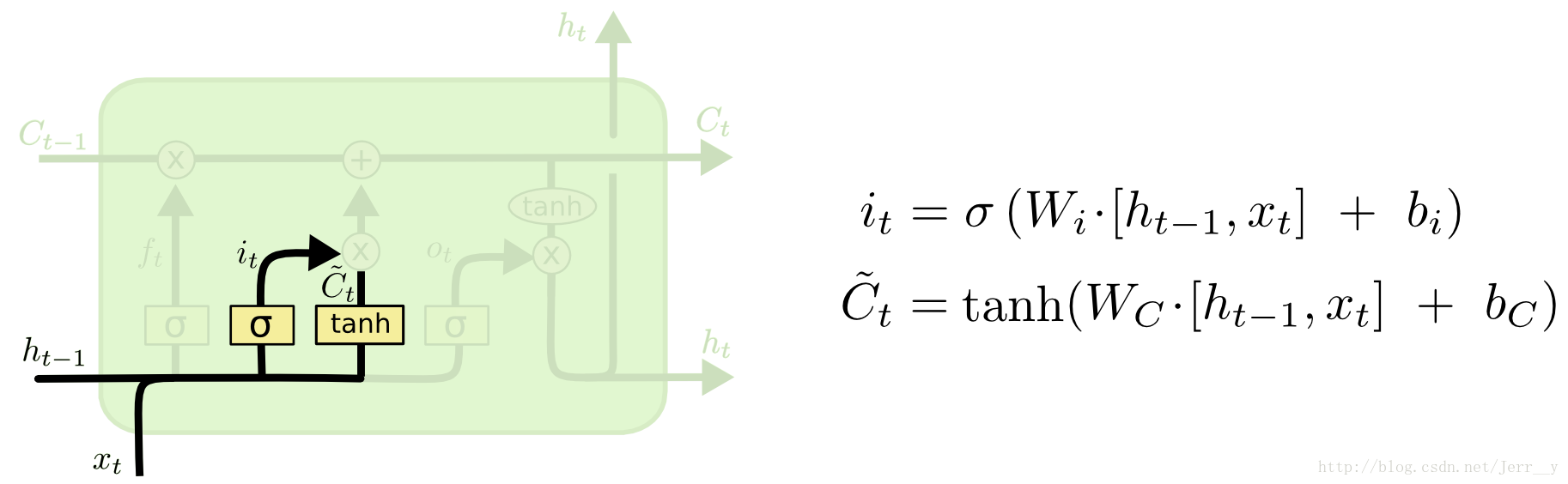
输入门
输入门决定让多少新的信息加入到当前cell的状态中。这分成两步:首先通过sigmoid函数得到输入门$i_t$,再通过tanh得到备选的要更新的内容。最后,联合这两部分,从而对当前cell的状态进行更新。
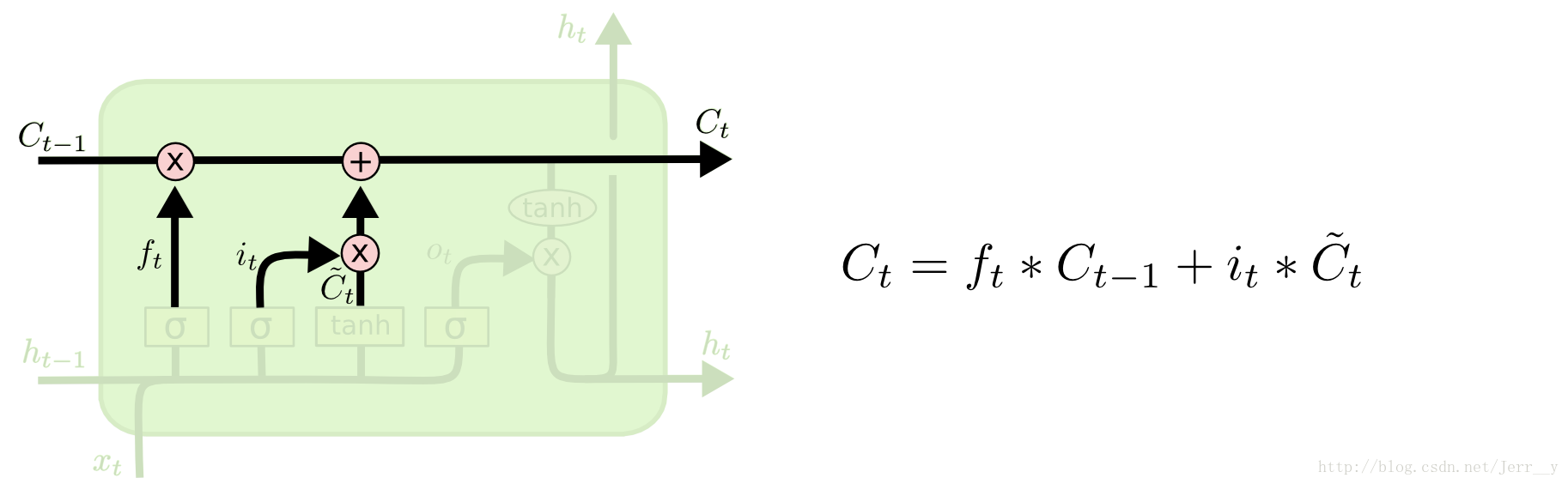
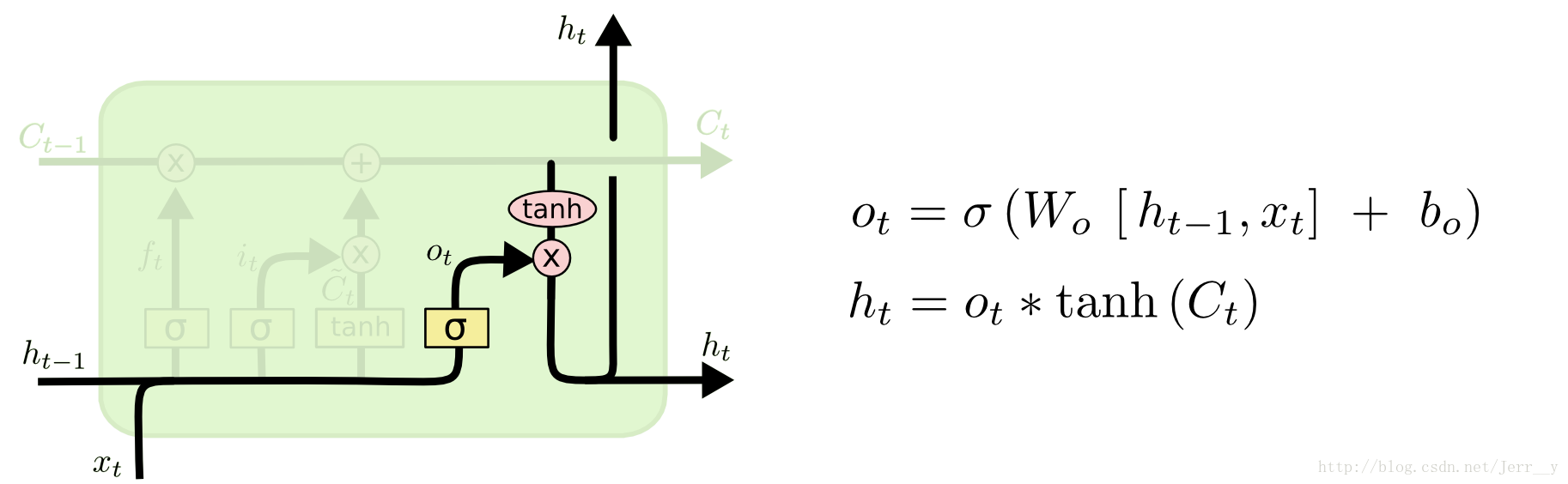
输出门
输出门决定要输出哪些信息,传递给下一个cell。当前cell的输出是依赖于$C_t$的值,但是不完全依赖于$C_t$的值,而是使用tanh函数对其进行了过滤。而输出门$o_t$通过sigmoid函数得到一个(0,1)的值,从而决定输出过滤后的$C_t$值的哪些部分。
LSTM变种—GRU

LSTM变种—peehole connection
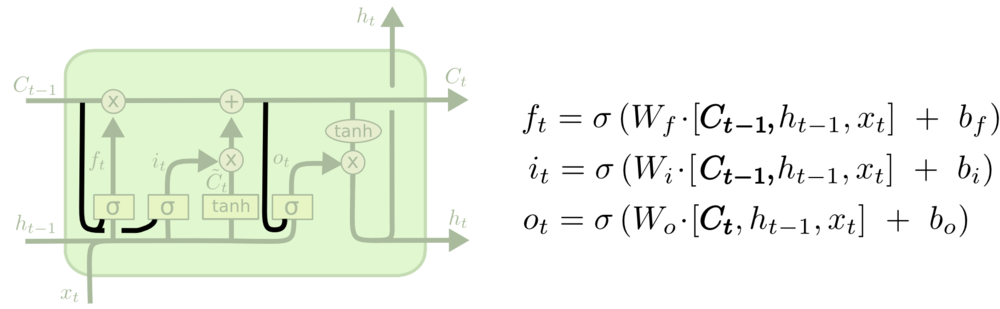
一些细节
1.LSTM为什么能够解决梯度消失?
答:秘诀就在这个公式: 。在RNN中,每个记忆单元h_t-1都会乘上一个W和激活函数的导数,这种连乘使得记忆衰减的很快,而LSTM是通过记忆和当前输入”相加”,使得之前的记忆会继续存在而不是受到乘法的影响而部分“消失”,因此不会衰减。因为LSTM对记忆的操作是相加的,线性的,使得不同时序的记忆对当前的影响相同,为了让不同时序的记忆对当前影响变得可控,LSTM引入了输入门和输出门,之后又有人对LSTM进行了扩展,引入了遗忘门。
2.RNN中为什么要使用tanh?为啥不使用Relu?
答:可以用,但是不用,原因有两个:1.relu函数的值域是0到无穷,如果直接直接把激活函数换成ReLU,会导致非常大的输出值,会造成溢出;2.使用relu仍然无法解决梯度在长程上传递的问题。当反向传播的时候,最后计算的结果会变成多个W连乘,如果W中存在特征值>1的,那么经过BPTT连乘后得到的值会爆炸,产生梯度爆炸的问题,使得RNN仍然无法传递较远距离。

