目前为止,已经学了很多东西,但是没有输出,总感觉似乎少了点什么。这片博客将回顾经典的Attention机制。Attention模型是深度学习领域最有影响力的工作之一,最初应用于图像领域(hard attention),后来在NMT任务上取得巨大成功后,便开始风靡于整个深度学习社区,尤其是在NLP领域。随后提出的GPT、ELMo、transformer、BERT、GPT-2、XLNET等模型,均有Attention机制的影子。本文将详细讲解两种经典的Attention模型:Bahdanau Attention与Luong Attention,并对Attention模型进行一个小小的总结。
为什么要有Attention机制?
真正的Attention机制源于神经机器翻译(NMT)。在NMT中,最常用的模型架构是:encoder-decoder。我们将输入序列输入到encoder部分,encoder最终输出一个固定长度的vector,从而作为decoder部分的输入,最终,decoder部分输出翻译后的结果。encoder-decoder架构如下图所示。
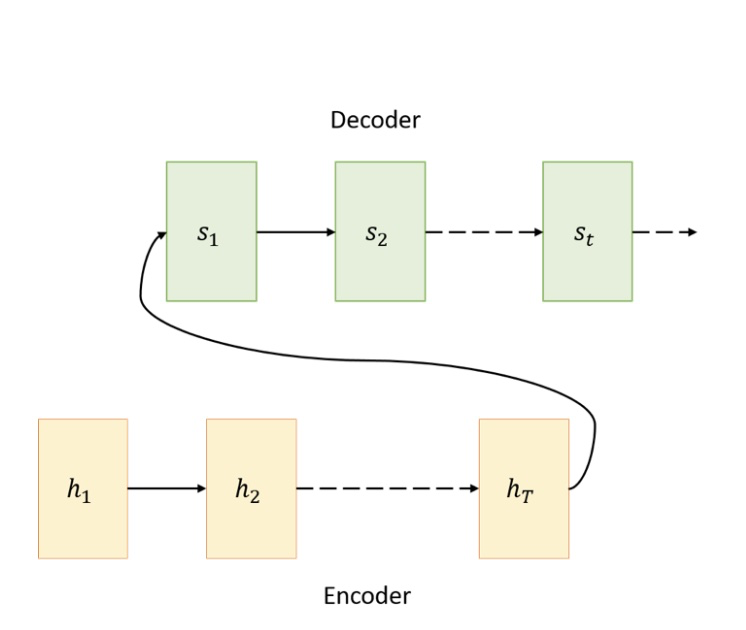
但是上述的encoder-decoder架构存在缺陷:输入序列不论长短,都会被编码成一个固定长度的vector,作为decoder的输入,而decoder的效果会受制于该vector。也就是说,上述架构要求当前状态记录到目前为止所有的信息,但是我们无法通过一个vector来保存所有序列的信息。这会限制整个模型的性能。尤其当源输入序列非常长的时候,模型的性能会下降地越迅速。在机器翻译任务上,就表现为:当输入序列非常长的时候,翻译的文本质量会非常差。这就引进了Attention模型。
传统的Attention模型有两种。一个是Dzmitry Bahdanau等人在《Neural Machine Translation by Jointly Learning to Align and Translate》论文中提出的Attention模型,简称:Bahdanau Attention;另一个是Minh-Thang Luong等人在《Effective Approaches to Attention-based Neural Machine Translation》论文中提出的Attention模型,简称:Luong Attention。下面将分别详细地介绍两种Attention模型。
Bahdanau Attention
首先给出Attention模型的架构图,如下所示。
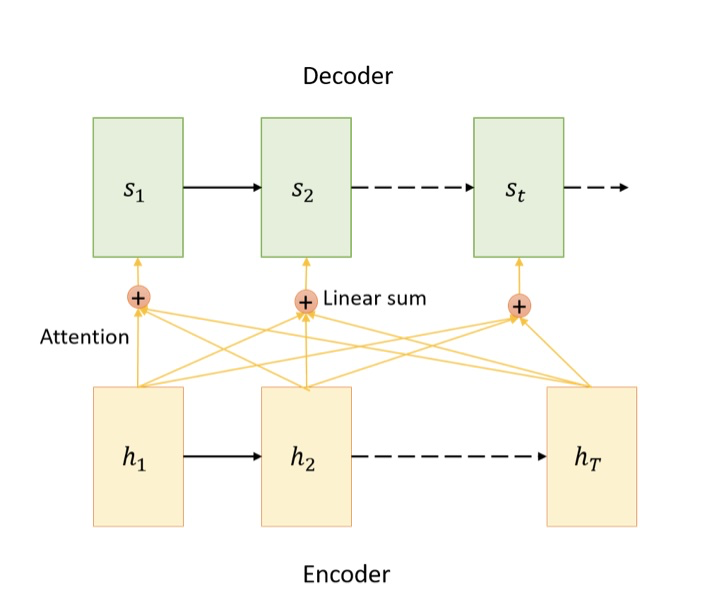
整个模型的计算,可分为以下几步:
- encoding
- 计算attention weights
- 计算context vector
- decoding
下面将详细地介绍每一个步骤。
Encoding
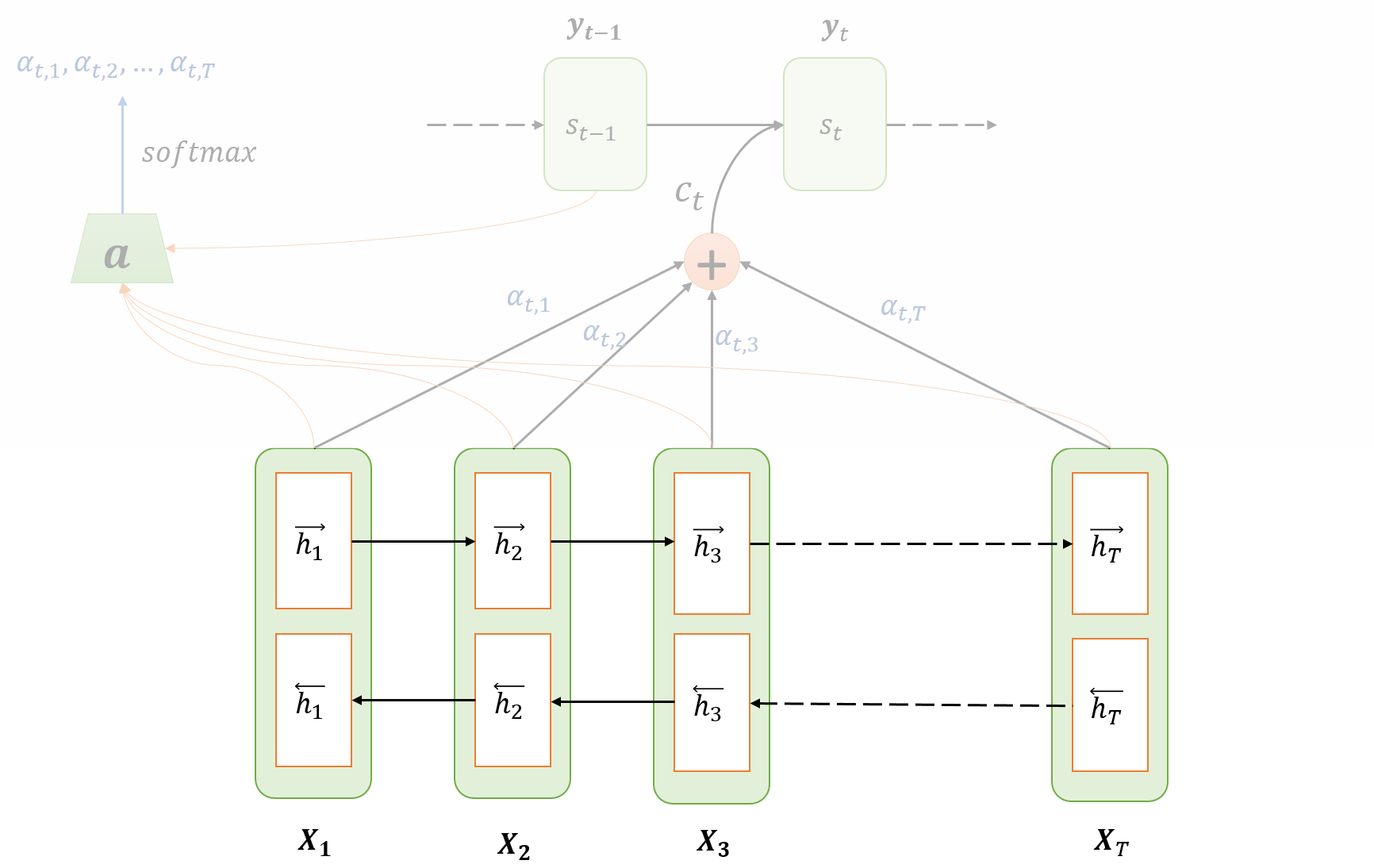
- 输入序列:$X=\{x_1,x_2,x_3,…,x_{T_X}\}$,其中$T_X$表示输入序列的长度。
- 在encoder部分,使用BRNN。,表示前向RNN的每一时间步的hidden state,亦可以叫做激活值;,表示反向RNN的每一时间步的hidden state,亦可以叫做激活值。(不懂BRNN的话,建议直接看论文或者Andrew Ng的《Deep Learning》。)
- 使用$h_j=(\overrightarrow h_j,\overleftarrow h_j)$表示encoder部分中j时刻的hidden state。
计算attention weights
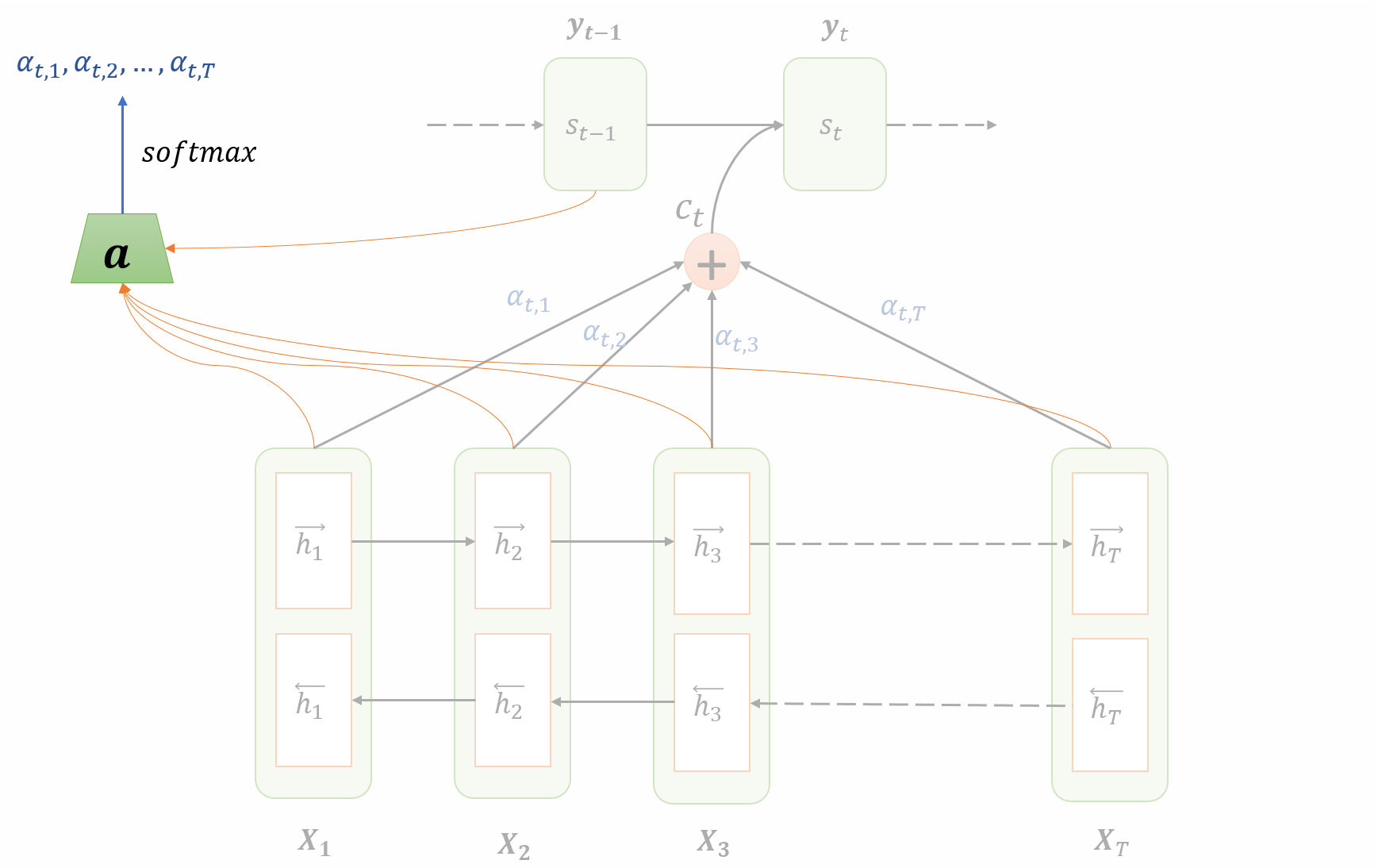
- Attention weights $\alpha_{t,j}$的含义是:在生成第t个输出的时候,应该在第j个encoder单元的注意力大小。Attention weights的计算公式如下:
这实际上就是通过softmax得到的attention的分布。
- 需要着重理解的是对齐模型(alignment model)。在这个公式中:$e_{t,j}=a(s_{t-1},h_j)$,a是对齐模型,用来评估当前预测词与输入序列中每一个输入词的相关度。直观地理解就是:在decoder的时候,我们更加关注于那些与预测词相关的部分。在生成一个预测词的时候,我们会考虑输入序列中每一个输入词与当前预测词的对齐关系(相关程度),对齐越好的词,我们应该给予它更大的权重,因为它对当前预测词的影响越大。
计算context vector
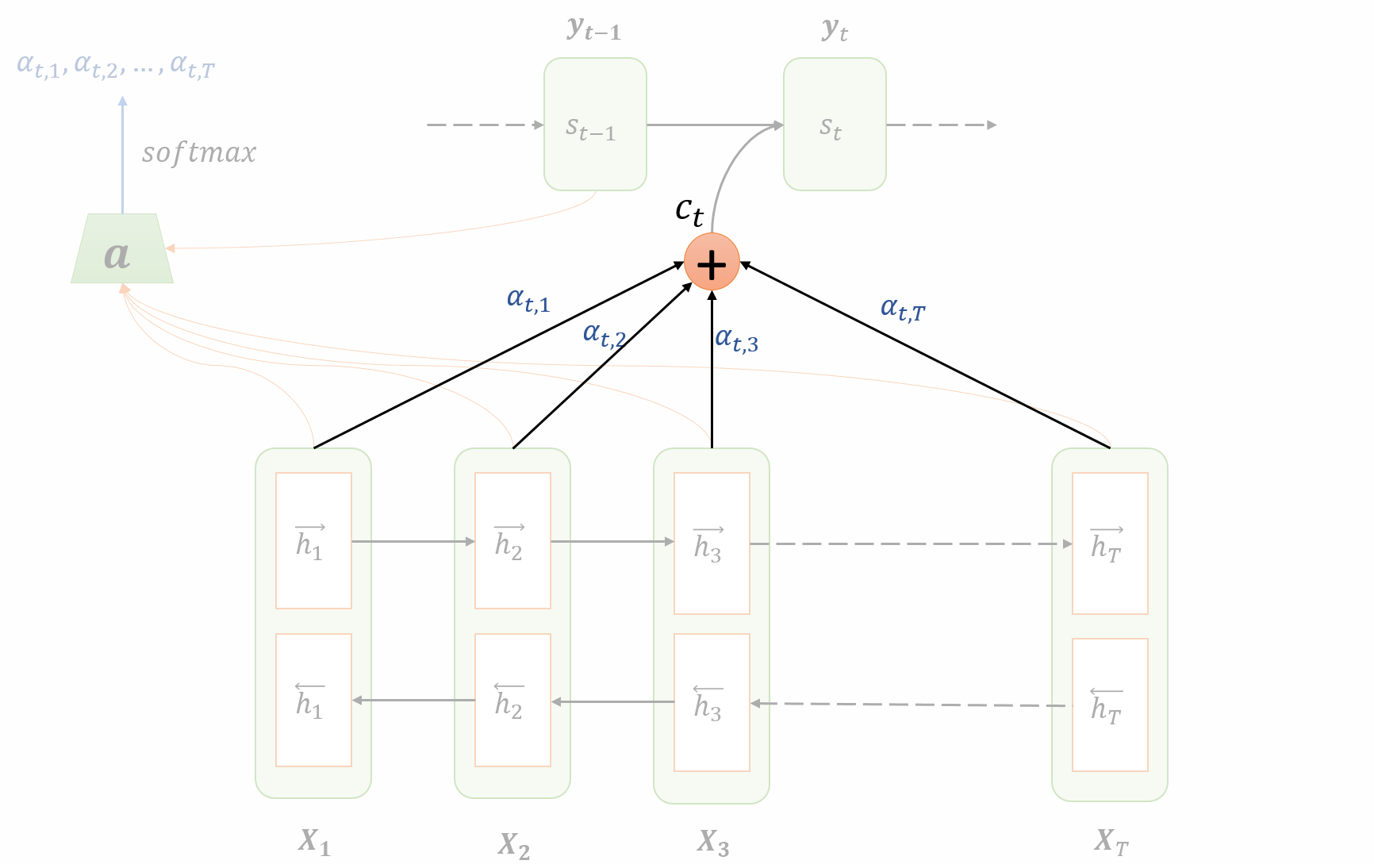
Context vector的计算非常简单,就是所有encoder部分的hidden state的加权平均,计算公式如下:
其中,$\alpha_{t,j}$就是Attention weights,$h_j$就是在encoder部分,计算的每一个时刻的hidden state。从这个式子可以知道,$\alpha_{t,j}$ 决定了$h_j$对$c_t$的影响。当$\alpha_{t,j}$ 越大,那么$h_j$对对$c_t$的影响就越大。
Decoding
通过上述几步,我们现在已经拥有的东西有:$h_j$、$c_t$、$s_{t-1}$、$\hat y_{t-1}$。接下来,我们就来计算t时刻的hidden state,并得到输出$\hat y_{t}$。计算公式如下:
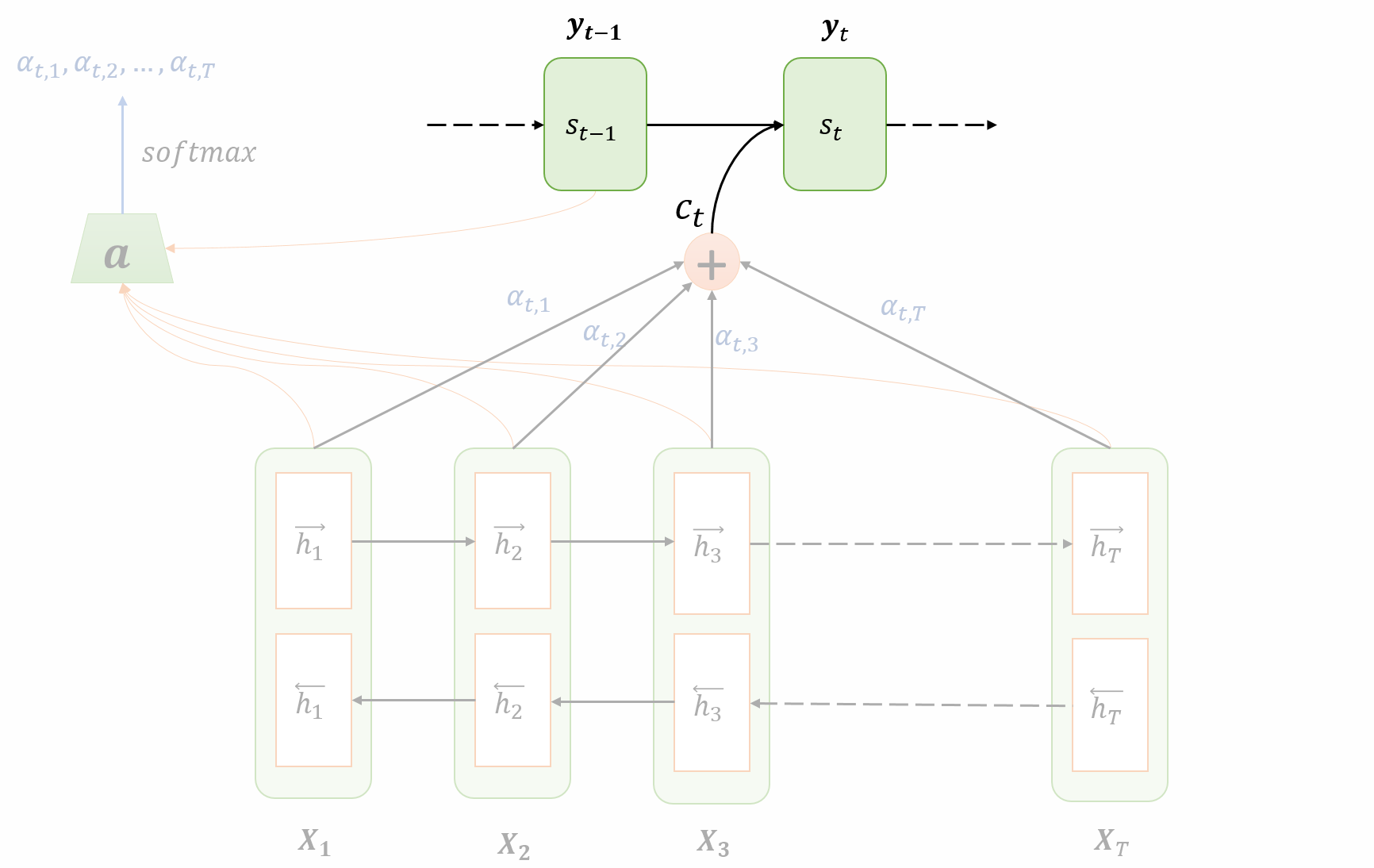
其中,g可以是GRU或者LSTM单元等,f可以是softmax单元等。
当然,在预测阶段,需要使用Beam Search,从而来得到最接近原意的翻译,在这,就不展开讨论了,等有时间,再写写关于Beam Search的文章~
至此,Bahdanau Attention的原理就讲解完毕了,其实回顾一下,整个过程一点都不复杂。
Luong Attention
Luong等人提出了新的更为简单和有效的Attention模型。整个模型又分为两个模型:global attention与local attention。global attention与local attention的本质区别在于:global attention使用整个输入序列的hidden state来计算context vector,而local attention只使用输入序列的hidden state的一个子集来计算context vector。下面将具体阐述这两种模型。
Global Attention
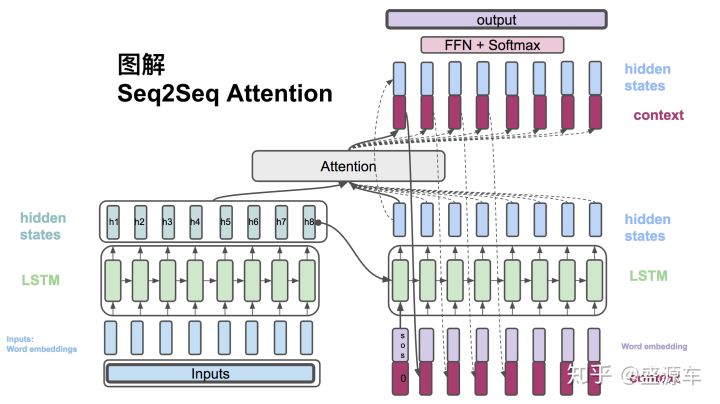
Global Attention实际上可以看作Bahdanau Attention的简化版本,但是又有些区别。具体步骤下面将一一介绍。
具体步骤有:
- encoding
- 计算decoder的hidden state
- 计算对齐向量,其实就是注意力权重
- 计算context vector
- 计算decoder每一个时刻最终的hidden state
- 计算输出
Encoding
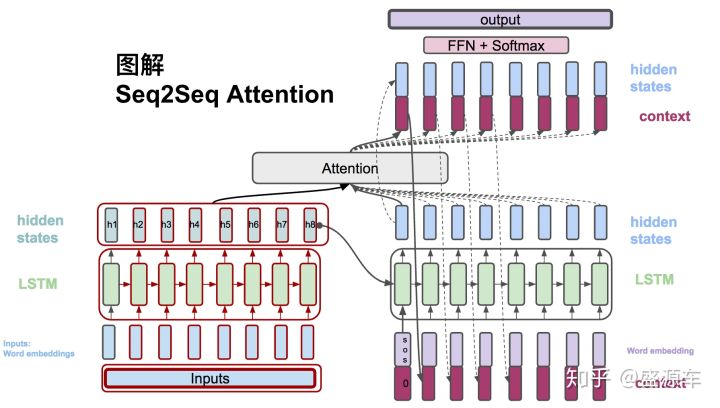
- 输入序列:$X=\{x_1,x_2,x_3,…,x_{T_X}\}$,其中$T_X$表示输入序列的长度。
- 计算encoder每一个时刻的hidden state,计算公式如下:
其中,$h_{t-1}$表示上一个时刻的hidden state,$x_t$表示t时刻的输入词的word embedding。
计算decoder的hidden state
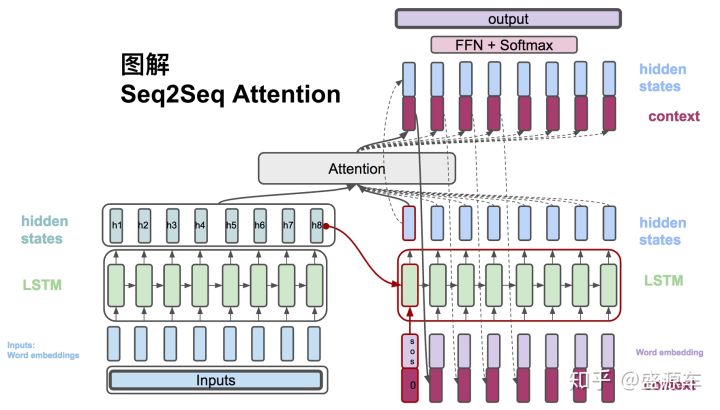
计算公式如下:
其中,$s_t$表示decoder中t时刻的hidden state,$s_{t-1}$表示decoder中t-1时刻的hidden state,$\hat y_{t-1}$表示decoder中t-1时刻的输出词的word embedding。
计算对齐向量,其实就是注意力权重
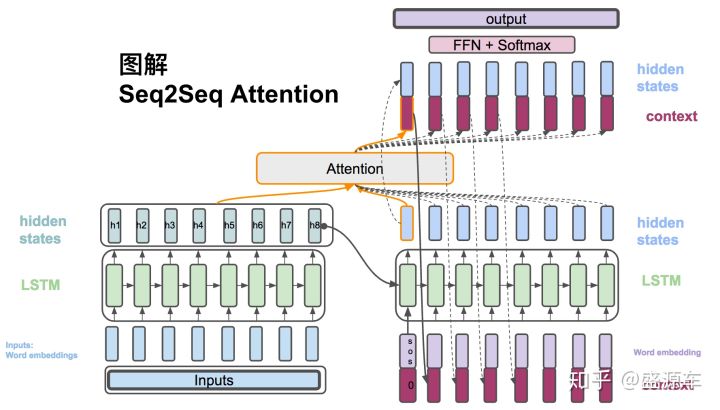
计算公式如下:
其中,$\alpha_{t,j}$是对齐向量,也就是注意力权重,表示生成预测词$\hat y_{t}$,需要在$h_j$上需要花费的注意力大小;$e_{t,j}$表示一个分数,通过score函数得到。score函数有三种方案(general方案效果最好),如下所示:
最后,我们会详细讲解score函数是如何工作的。
计算context vector

context vector的计算公式如下:
其中,$\alpha_{t,j}$表示对齐向量,也就是注意力权重,$h_j$表示encoder中j时刻的hidden state。
计算decoder中每一个时刻最终的hidden state
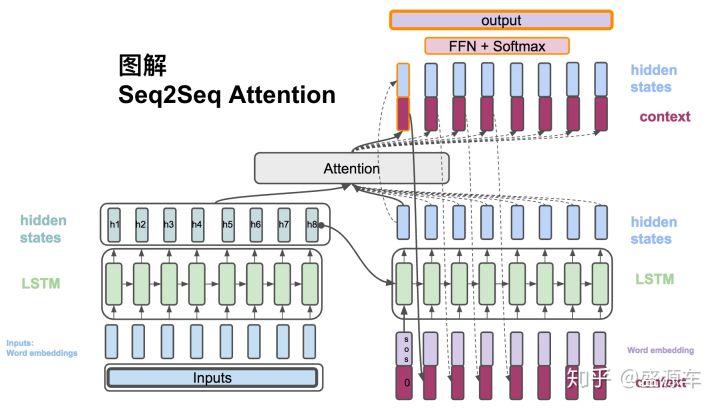
将context vector 和 decoder的hidden states 串起来。计算公式如下:
计算输出
context vector和decoder的hidden state合起来通过一系列非线性转换以及softmax最后计算出概率。计算公式如下:
在下一个时刻,将$s_t$、$\hat y_t$作为第二个节点的输入,循环上述过程。在论文中,还将$\hat s_t$作为第二个节点的输入,用来辅助当前节点的对齐决策过程。过程如下图所示。
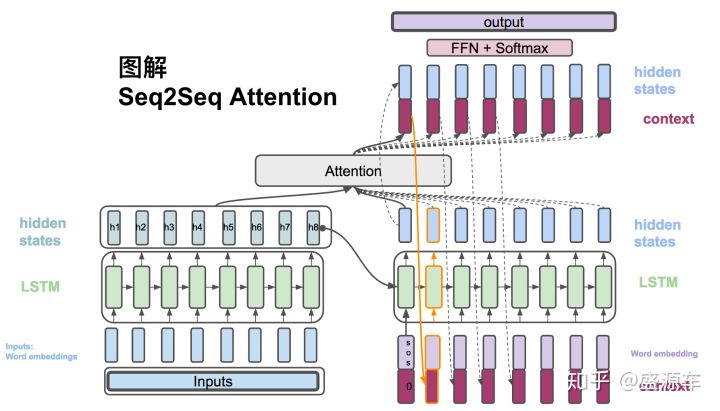
关于global attention,还有一个没有讲的知识点,就是score函数是如何工作的。下面以dot与general为例,进行说明。
dot
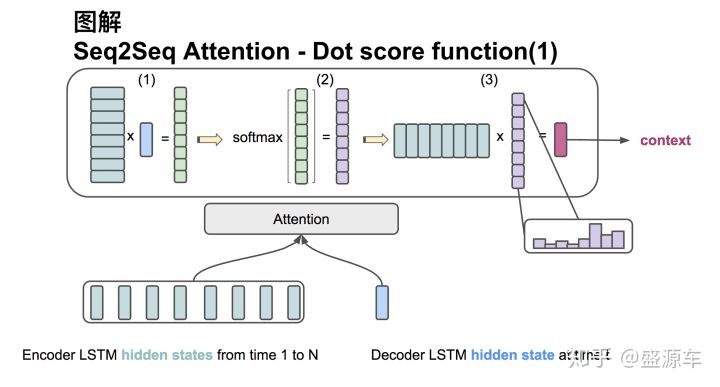
过程:
注意,下面描述部分可能与前面公式不符合,是因为前面的公式的表示是用加权平均和来表示,而下面描述是用矩阵相乘来描述的,所以是没有问题的!
输入分为两部分:1.encoder中所有的hidden state H,维度是: (hid dim1 ,sequence length);2.decoder中在同一时刻的hidden state s,其维度是: (hid dim1,1)。
第一步:转置H,再与s点乘,得到维度为(sequence,1)的分数;
第二步:对分数进行softmax,得到和为1的权重(对齐向量);
第三步:将H与第二步得到的分数相乘,得到(dim1,1)的context vector。
general
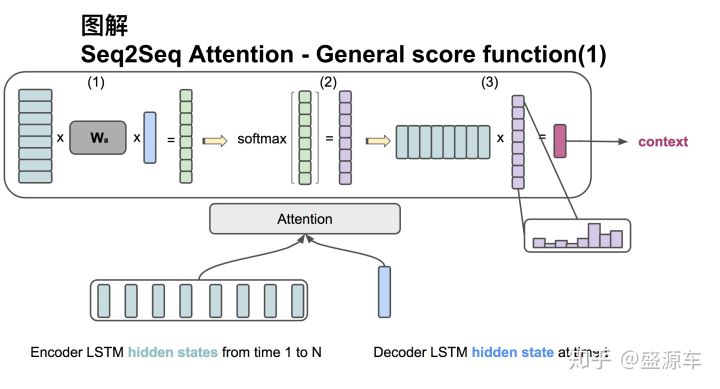
过程:
注意,下面描述部分可能与前面公式不符合,是因为前面的公式的表示是用加权平均和来表示,而下面描述是用矩阵相乘来描述的,所以是没有问题的!
输入分为两部分:1.encoder中所有的hidden state H,维度是: (hid dim1 ,sequence length);2.decoder中在同一时刻的hidden state s,其维度是: (hid dim2,1)。二者维度并不一样!
第一步:转置H为(sequence length,hid dim1),再与$W_a$相乘,$W_a$的维度:(hid dim1,hid dim2),最后再与$s$做点乘,得到一个(sequence,1)的分数;
第二步:对分数进行softmax,得到和为1的权重(对齐向量);
第三步:将H与第二步得到的分数做点乘,得到(hid dim2,1)的context vevtor。
Local attention
local attention是soft attention与hard attention的一种折衷方案。其在计算context vector的时候,每次只考虑encoder中所有hidden state的一个子集。由于local attention与global attention十分类似,下面将着重介绍其与global attention不同的地方,相同部分就省略了。
local attention在计算context vector的时候,只考虑encoder中所有hidden state的一个子集。那么如何找到这个子集呢?local attention的做法如下:
local attention针对t时刻的输出,生成一个他在源输入序列中的对齐位置$p_t$,接着在源输入序列中选取一个窗口:$[p_t-D,p_t+D]$,其中$D$根据经验给出。context vector的计算则根据窗口内所有的hidden state的加权平均得到。
那么如何得到这个对齐位置$p_t$呢?local attention给出了两种方法,如下:
- 单一对齐:即简单粗暴地设置$p_t=t$,对齐向量与context vector的计算公式,与前面的公式一样:$\alpha_{t,j}=\frac {exp(e_{t,j})}{\sum_{k={p_t-D}}^{p_t+D}exp(e_{t,k})}$,$c_t=\sum_{j=p_t-D}^{p_t+D}\alpha_{t,j}h_j$。
- 预测对齐:针对每个预测词,预测其在源输入序列中的对齐位置。公式如下:
其中,$S$表示源输入序列的长度,所以$p_t$的大小在区间$[0,S]$之间。
Luong attention到此就讲完了,总结一下:
luong attention是bahdanau attention的简化版本,而且计算代价也更小。global attention与bandanau attention非常的类似,只是计算路径不同,global attention的计算路径是: $s_t->\alpha_t(s)->c_t->\hat s_{t}$;bahdanau attention的计算路径是:$s_{t-1}->\alpha_{t}(s)->c_t->s_{t}$。
local attention是soft attention与hard attention的折衷方案,与global 不同的地方在于:计算context vector的时候,只考虑encoder中所有hidden state的子集,其余部分一样。
Attention机制总结
Soft Attention:指的是在求注意力权重的时候,对于源输入序列中的每一个词都给予权重;
Hard Attention:直接从输入句子里面找到某个特定的单词,然后把目标句子单词和这个单词对齐,而其它输入句子中的单词硬性地认为对齐概率为0。
Global attention属于soft attention;
local Attention严格来说也属于soft attention,但是一般看作是soft和hard的一种结合;
还有 attention over attention、self -attention等等。
关于attention的应用非常多,之后有机会还会再写写关于Attention的文章~
参考文献
- 《Neural Machine Translation by Jointly Learning to Align and Translate》
- 《Effective Approaches to Attention-based Neural Machine Translation》
- https://medium.com/@shashank7.iitd/understanding-attention-mechanism-35ff53fc328e
- https://zhuanlan.zhihu.com/p/40920384

