常用的数据结构。
动态规划|股票购买问题
以123买卖股票的最佳时机为例,进行剖析。
1.总体思路:穷举,或者说是状态机
在该题中,总共有三种状态:天数、可以进行的交易的数目、持有状态。然后遍历所有状态,从而得到最后的结果。(其实就是穷举的思路)代码如下:

以这道题为例,$dp[i][k][1]$ 表示在第$i$天,此刻持有股票,至今为止总共进行过$k$次交易,这个时候的总利润;$dp[i][k][0]$ 表示在第 $i$ 天,此刻没有持有股票,至今为止总共进行过$k$次交易,这个时候的总利润。
2.状态转移框架
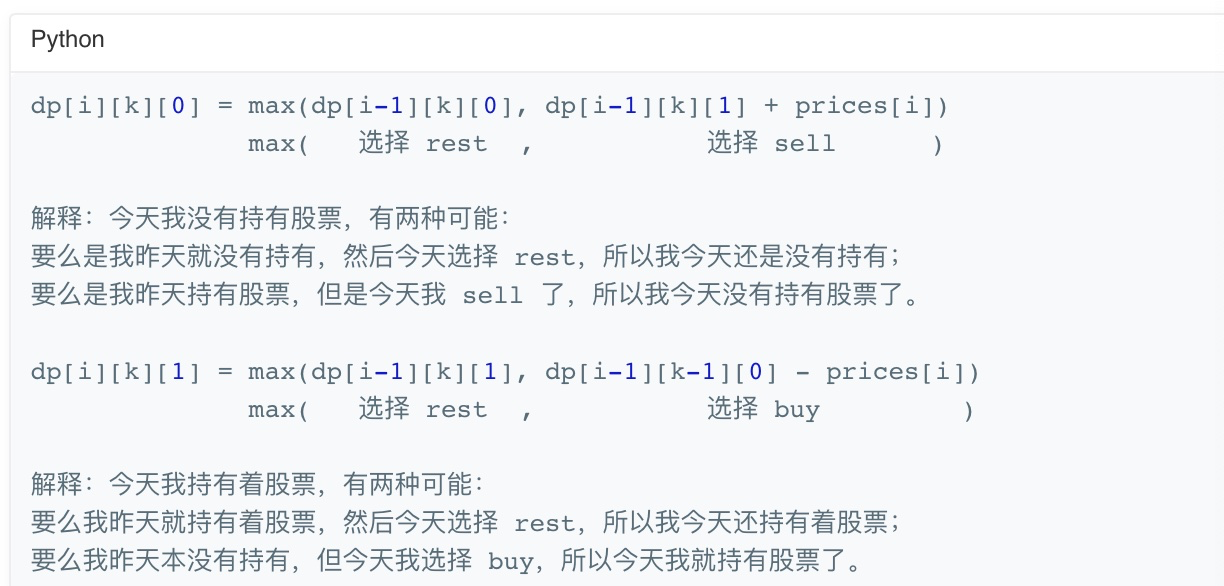
上述图片解释了状态转移框架。在这里,需要注意两点:
第一:在计算的时候,我们需要用到,在这里,需要将$k$变成$k-1$,因为正是因为在$i-1$天没有进行持有股票,那么经过一次交易后,才会在$i$天持有股票,那么自然而言的,交易次数要增加1.
第二:在从无到持有股票的过程中,需要减去股票的价值;而反过程中,需要加上股票的价值。
3.base case的处理
状态转移方程:
在状态转移方程当中,当$i=0$的时候,需要计算$dp[-1]$。那么实际上index为-1,其实是有问题的,所以我们需要通过一些方法处理这些case。
实际上,处理这些base case,也是根据状态转移方程来进行分析。当$i=0$的时候,其状态转移方程为下:
那么具体分析上述方程的细节。$dp[-1][k][0]$表示的是第-1天的时候,不持有股票。那么实际上天数是从第0天开始的,当$i=-1$的时候,意味着还没有开始。所以:$dp[-1][k][0]=0$。$dp[-1][k-1][1]$表示是在第-1天的时候,持有股票。实际上,当还没有开始的时候,是不可能持有股票的。所以:$dp[-1][k-1][1]=-infinity$
。其他的依次类推。
4.程序代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
| #include<stdio.h>
#include<string.h>
#include<string>
#include<algorithm>
#include<iostream>
#include<vector>
#define INF 0x3f3f3f3f
#define NINF -INF-1
using namespace std;
class Solution{
public:
int maxProfit(vector<int>& prices) {
int n=prices.size();
if(n==0){
return 0;
}
int k_max=2;
int dp[n+1][k_max+1][2];
memset(dp,0,sizeof(dp));
for(int i=0;i<n;i++){
for(int k=k_max;k>=1;k--){
if(i-1==-1){
dp[i][k][0]=0;
dp[i][k][1]=-prices[i];
continue;
}
dp[i][k][0]=max(dp[i-1][k][0],dp[i-1][k][1]+prices[i]);
dp[i][k][1]=max(dp[i-1][k][1],dp[i-1][k-1][0]-prices[i]);
}
}
return dp[n-1][k_max][0];
}
};
int main(){
int n;
scanf("%d",&n);
vector<int> prices;
for(int i=0;i<n;i++){
int x;
scanf("%d",&x);
prices.push_back(x);
}
Solution so1;
int ans = so1.maxProfit(prices);
printf("%d\n",ans);
return 0;
}
|
其他的关于股票的问题还有:121. 买卖股票的最佳时机、122. 买卖股票的最佳时机 II、188. 买卖股票的最佳时机 IV、309. 最佳买卖股票时机含冷冻期、714. 买卖股票的最佳时机含手续费。套用框架均可以解决。
OK,终于写完了~🤩☕️
DFS(二叉树路径和问题)
给定一棵二叉树,你需要计算它的直径长度。一棵二叉树的直径长度是任意两个结点路径长度中的最大值。这条路径可能穿过也可能不穿过根结点。
示例 :
给定二叉树
1
/ \
2 3
/ \
4 5
返回 3, 它的长度是路径 [4,2,1,3] 或者 [5,2,1,3]。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
|
class Solution {
public:
int diameterOfBinaryTree(TreeNode* root) {
if(root==nullptr) return 0;
int ans=0;
depth(root,ans);
return ans-1;
}
int depth(TreeNode * root,int &ans){
if(root==0) return 0;
int l=depth(root->left,ans);
int r=depth(root->right,ans);
ans=max(ans,l+r+1);
return max(l,r)+1;
}
};
|
给定一个非空二叉树,返回其最大路径和。
本题中,路径被定义为一条从树中任意节点出发,沿父节点-子节点连接,达到任意节点的序列。该路径至少包含一个节点,且不一定经过根节点。
示例 1:
输入:[1,2,3]
1
/ \
2 3
输出:6
示例 2:
输入:[-10,9,20,null,null,15,7]
-10
/ \
9 20
/ \
15 7
输出:42
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
|
class Solution {
public:
int maxPathSum(TreeNode* root) {
if(root==nullptr) return 0;
int ans=root->val;
helper(root,ans);
return ans;
}
int helper(TreeNode * root,int &ans){
if(root==nullptr) return 0;
int l=max(0,helper(root->left,ans));
int r=max(0,helper(root->right,ans));
ans=max(ans,l+r+root->val);
return max(l,r)+root->val;
}
};
|
给定一个二叉树,找到最长的路径,这个路径中的每个节点具有相同值。 这条路径可以经过也可以不经过根节点。
注意:两个节点之间的路径长度由它们之间的边数表示。
示例 1:
输入:
5
/ \
4 5
/ \ \
1 1 5
输出:
2
示例 2:
输入:
1
/ \
4 5
/ \ \
4 4 5
输出:
2
注意: 给定的二叉树不超过10000个结点。 树的高度不超过1000。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
|
class Solution {
public:
int longestUnivaluePath(TreeNode* root) {
if(root==nullptr) return 0;
int ans=1;
dfs(root,ans);
return ans-1;
}
int dfs(TreeNode * root,int &ans){
if(root==nullptr) return 0;
int l=dfs(root->left,ans);
if(l!=0 && root->left->val != root->val) l=0;
int r=dfs(root->right,ans);
if(r!=0 && root->right->val != root->val) r=0;
ans=max(ans,l+r+1);
return max(l,r)+1;
}
};
|



